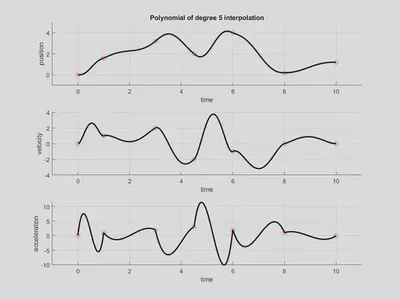
机器人轨迹规划的多项式插值法 / Robot Trajectory Planning with Polynomial Interpolation
该博文参考自: https://zhuanlan.zhihu.com/p/269230598
问题定义
给定一些离散的数据点,我们需要通过插值的方式生成一条能够通过所有给定数据点的参考曲线。
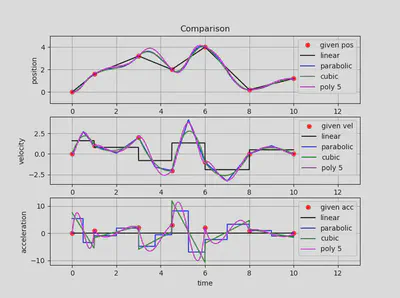
根据实际应用,对于“平滑”的要求通常会有以下不同的约束:
- 要求生成的参考曲线是连续的;
- 在(1)的基础上,要求参考曲线的速度是连续的;
- 在(1)和(2)的基础上,要求参考曲线的加速度是连续的;
注意:速度是位置对时间的导数,加速度是速度对时间的导数,加速度对时间的导数我们称之为jerk。
通常情况下,在机器人高速运动的时候,想要得到非常连续、平滑、噪音低的运动控制,第3个约束条件是必不可少的,有的甚至还要求加速度的导数jerk都是连续的。
在多项式插值里面,给定多项式的阶次越高,能拟合的函数曲线就越复杂,但越高阶次的多项式对于计算资源的要求越多。因此对于这3个要求,我们可以分别用不同阶次的多项式函数来拟合,实际应用时根据需求选择合适的方法。
线性插值(一阶,速度恒定)
线性插值将给定的数据点依次用线段连起来,点与点之间运动的速度是恒定值。假设我们用$q(t)$来表示插值以后的曲线,则用数学的方式来表示线性插值就是:
$$
q(t) = a_0 + a_1 (t-t_0)
$$
其中,$a_0$、$a_1$是待确定的常量参数。$t_0$表示初始时刻,$a_0$表示初始时刻的位置,$a_1$表示斜率,也就是速度,这里为常量。因此,给定下一个时刻$t_1$处的位置$q(t_1)$,我们有:
$$
\begin{cases}
q(t_0) = q_0 = a_0
\\
q(t_1) = q_1 = a_0 + a_1(t_1 - t_0)
\end{cases}
$$
由此我们可以计算得到两个常量参数:
$$
\begin{cases}
a_0 = q_0
\\
a_1 = (q_1 - q_0) / (t_1 - t_0)
\end{cases}
$$
曲线的速度为:
$$
\dot{q}(t) = a_1
$$
示例
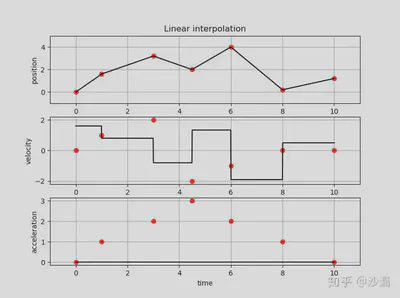
红圈内为给定的中间点值,黑色实线为插值的结果。
从图中可以明显地看到,线性插值带来的最大问题就是在各个 拐弯处其速度不连续,因此对于运动控制来说,在这里会有一个速度的阶跃。例如,对于电机来说,这里会导致控制电流急剧变化,使得电机的输出不稳定,从而引发“抖动”问题,严重者还会损坏机构本身。因此,线性插值本身的问题导致其在控制领域应用范围受限。
抛物线插值(二阶,恒定加速度)
抛物线差值(Parabolic Spline)是二阶多项式插值方法。与线性插值法将各个数据点用线段连起来不同,抛物线插值方法是用二次曲线将各个数据点连接起来,在连接处使用平滑的曲线来过渡,而避免速度不连续导致的“急剧拐弯”。抛物线差值的特征是具有恒定的加速度/减速度,一般是由两个多项式的组合来得到。为什么是两个多项式呢?因为一个用于“加速阶段”,一个用于“减速阶段”。“加速阶段”和“减速阶段”的分割点叫Flex Point。
考虑2个数据点之间插值的情况。假设初始时刻是$t_0$, 在flex point处对应的时刻是$t_f$,最终时刻为$t_1$。
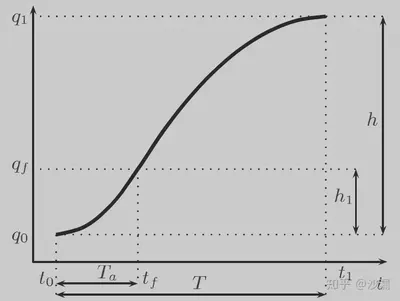
先来看一个特殊情况,flex point的位置是起点和终点的中间位置(也可以任意设定,后面我们会讨论,这里先讨论在中间位置的情况),即
$$
t_f = \frac{t_0 + t_1}{2}
$$
$$
q_f = \frac{q_0 + q_1}{2}
$$
此外我们作几个符号定义:
$$
h = q_1 - q_0
\\
T = t_1 - t_0
\\
T_a = t_f - t_0
\\
h_1 = q_f - q_0
$$
加速阶段
对于加速阶段,其数学表达式为:
$$
q_a(t) = a_0 + a_1(t - t_0) + a_2(t - t_0)^2 , t \in [t_0,t_f]
$$
其中$a_0$、$a_1$、$a_2$是待确定的常量参数,当我们给定$q_0 = q_a(t_0)$和$q_f = q_a(t_f)$以及初始时刻的速度$v_0$以后,有如下关系:
$$
\begin{aligned}
q_a(t_0) &= q_0 = a_0
\\
q_a(t_f) &= q_f = a_0 + a_1(t_f - t_0) + a_2(t_f - t_0)^2
\\
\dot{q}_a(t = t_0) &= a_1 + 2a_2(t_0 - t_0) = a_1 = v_0
\end{aligned}
$$
因此,常量参数可以计算为:
$$
\begin{aligned}
a_0 &= q_0
\\
a_1 &= v_0
\\
a_2 &= \frac{q_f - q_0 - v_0(t_f - t_0)}{(t_f - t_0)^2} = \frac{h_1 - v_0 T_a}{T_a^2} = \frac{2(h - v_0 T)}{T^2}
\end{aligned}
$$
这样,我们可以计算得到当$t \in [t_0,t_f]$时,插值曲线为:
$$
\begin{aligned}
q_a(t) &= q_0 + v_0(t - t_0) + \frac{2(h - v_0 T)}{T^2}(t - t_0)^2
\\
\dot{q}_a(t) &= v_0 + \frac{4(h - v_0 T)}{T^2}(t - t_0)
\\
\ddot{q}_a(t) &= \frac{4(h - v_0 T)}{T^2}
\end{aligned}
$$
在flex point的速度可以这样计算:
$$
\begin{aligned}
v_{max} &= \dot{q}_a(t_f) = v_0 + \frac{4(h - v_0 T)}{T^2}(t_f - t_0)
\\
&= v_0 + \frac{4(h - v_0 T)}{T^2} \cdot \frac{T}{2}
\\
&= v_0 + \frac{2h}{T} - 2v_0
\\
&= \frac{2h}{T} - v_0
\end{aligned}
$$
与线性插值不同的是,除了指定初始时刻的位置,我们还需要给定初始时刻的速度$v_0$。
在flex point处,由加速阶段进入减速阶段,因此此时加速度的符号是会反转的,会导致加速度不连续。
减速阶段
对于减速阶段,其数学表达式为:
$$
q_b(t) = a_3 + a_4(t - t_f) + a_5(t - t_f)^2 , t \in [t_f,t_1]
$$
其中,$a_3, a_4, a_5$为待定的常量参数。如果给定最终时刻的速度$v_1$,则有如下关系:
$$
\begin{aligned}
q_b(t_f) &= q_f = a_3
\\
q_b(t_1) &= q_1 = a_3 + a_4(t_1 - t_f) + a_5(t_1 - t_f)^2
\\
\dot{q}_b(t_1) &= v_1 = a_4 + 2a_5(t_1 - t_f)
\end{aligned}
$$
因此,我们可以计算得到:
$$
\begin{aligned}
a_3 &= q_f = \frac{q_0 + q_1}{2}
\\
a_4 &= 2\frac{h}{T} - v_1
\\
a_5 &= \frac{2(v_1T - h)}{T^2}
\end{aligned}
$$
这样,当$t \in [t_f,t_1]$时,插值曲线为:
$$
\begin{aligned}
q_b(t) &= q_f + (2\frac{h}{T} - v_1)(t - t_f) + \frac{2(v_1T - h)}{T^2}(t - t_f)^2
\\
\dot{q}_b(t) &= 2\frac{h}{T} - v_1 + \frac{4(v_1T - h)}{T^2}(t - t_f)
\\
\ddot{q}_a(t) &= \frac{4(v_1T - h)}{T^2}
\end{aligned}
$$
由此可以发现当$v_0 \neq v_1$,那么在$t = t_f$(flex point)处,速度曲线是不连续的。
当Flex Point处于任意位置时
加速度对称
此时$t_f = \frac{t_0 + t_1}{2}, q_f \neq \frac{q_0 + q_1}{2}$。那么为了保证速度曲线的连续,即$\dot{q}_a(t_f) = \dot{q}_b(t_f)$,我们有以下关系:
$$
\begin{aligned}
q_a(t_0) &= a_0 &= q_0
\\
\dot{q}_a(t_0) &= a_1 &= v_0
\\
q_b(t_1) &= a_3 + a_4\frac{T}{2} + a_5(\frac{T}{2})^2 &= q_1
\\
\dot{q}_b(t_1) &= a_4 + 2a_5\frac{T}{2} &= v_1
\\
q_a(t_f) &= q_b(t_f) = a_0 + a_1\frac{T}{2} + a_2(\frac{T}{2})^2 = a_3
\\
\dot{q}_a(t_f) &= \dot{q}_b(t_f) = a_1 + 2a_2\frac{T}{2} = a_4
\\
T/2 &= t_f - t_0 = t_1 - t_f
\end{aligned}
$$
联立以上多项式我们可以得到:
$$
\begin{aligned}
a_0 &= q_0
\\
a_1 &= v_0
\\
a_2 &= \frac{4h - T(3v_0 + v_1)}{2T^2}
\\
a_3 &= \frac{4(q_0 + q_1) + T(v_0 - v_1)}{8}
\\
a_4 &= \frac{4h - T(v_0 + v_1)}{2T}
\\
a_5 &= \frac{-4h + T(v_0 + 3v_1)}{2T^2}
\end{aligned}
$$
插值的结果中,加速度并不恒定,在$t = t_f$时刻,加速度存在一个阶跃,但加速度和减速度的绝对值是一样的,因此,这种情况属于加速度对称的情况,加速时间和减速时间也一致,都为$\frac{t_f - t_0}{2}$。
加速度不对称
由于抛物线插值的加速度恒定,所以加速度不对称也就表示加速时间和减速时间不一致,$t_f \in (t_0,t_1)$可以是区间内的任意值。此时,我们可以结合前面的两个多项式来构造插值的曲线:
$$
q_a(t) = a_0 + a_1(t - t_0) + a_2(t - t_0)^2 , t \in [t_0,t_f]
\\
q_b(t) = a_3 + a_4(t - t_f) + a_5(t - t_f)^2 , t \in [t_f,t_1]
$$
给定初始时刻$t_0$和最终时刻$t_1$处的位置和速度信息,且给定在$t_f$处要保证位置和速度曲线的连续性,则我们可以计算得到插值曲线:
$$
\begin{aligned}
q_a(t_0) &= a_0 &= q_0
\\
\dot{q}_a(t_0) &= a_1 &= v_0
\\
q_b(t_1) &= a_3 + a_4(t_1 - t_f) + a_5(t_1 - t_f)^2 &= q_1
\\
\dot{q}_b(t_1) &= a_4 + 2a_5(t_1 - t_f) &= v_1
\\
q_a(t_f) &= q_b(t_f) = a_0 + a_1(t_f - t_0) + a_2(t_f - t_0)^2 = a_3
\\
\dot{q}_a(t_f) &= \dot{q}_b(t_f) = a_1 + 2a_2(t_f - t_0) = a_4
\end{aligned}
$$
设加速时间为$T_a = t_f - t_0$,减速时间为$T_d = t_1 - t_f$,则由上述多项式可以计算得到:
$$
\begin{aligned}
a_0 &= q_0
\\
a_1 &= v_0
\\
a_2 &= \frac{2h - v_0(T + T_a) - v_1T_d}{2T T_a}
\\
a_3 &= \frac{2q_1T_a + T_d(2q_0 + T_a(v_0 - v_1))}{2T}
\\
a_4 &= \frac{2h - v_0T_a - v_1T_d}{T}
\\
a_5 &= - \frac{2h - v_0T_a - v_1(T + T_d)}{2T T_d}
\end{aligned}
$$
因此,在加速阶段,曲线的速度和加速度可以计算为:
$$
\begin{aligned}
\dot{q}_a(t) &= a_1 + 2a_2(t-t_0) = v_0 + \frac{2h - v_0(T + T_a) - v_1T_d}{T T_a}(t - t_0)
\\
\ddot{q}_a(t) &= 2a_2 = \frac{2h - v_0(T + T_a) - v_1T_d}{T T_a}
\end{aligned}
$$
在减速阶段,曲线的速度和加速度可以计算为:
$$
\begin{aligned}
\dot{q}_b(t) &= a_4 + 2a_5(t-t_f) = \frac{2h - v_0T_a - v_1T_d}{T} - \frac{2h - v_0T_a - v_1(T + T_d)}{T T_d}(t - t_f)
\\
\ddot{q}_b(t) &= 2a_5 = \frac{2h - v_0T_a - v_1(T + T_d)}{T T_d}
\end{aligned}
$$
如果 $v_0 = v_1 = 0$,那么就与前面加速度对称的情况结果一致了。
五次多项式插值(五阶,加速度连续)
考虑2个数据点之间插值的情况,与其他阶次的多项式形式类似,五次多项式插值方法的数学表达式为: $$ q(t) = a_0 + a_1(t - t_0) + a_2(t - t_0)^2 + a_3(t - t_0)^3 + a_4(t - t_0)^4 + a_5(t - t_0)^5 $$
其中,$a_0, a_1, ..., a_5$ 为待确定的参数。这里我们一共需要6个约束条件,即起点 $t_0$ 和终点 $t_1$ 的位置、速度和加速度信息。即给定如下条件:
$$
\begin{cases}
q(t_0) = q_0
\\
\dot{q}(t_0) = v_0
\\
\ddot{q}(t_0) = a_0
\\
q(t_1) = q_1
\\
\dot{q}(t_1) = v_1
\\
\ddot{q}(t_1) = a_1
\end{cases}
$$
设$T = t_1 - t_0$, $h = q_1 - q_0$, 则我们可以计算得到: $$ \begin{cases} a_0 = q_0 \\ a_1 = v_0 \\ a_2 = \frac{1}{2}a_0 \\ a_3 = \frac{1}{2T^3}[20h - (8v_1 + 12v_0)T - (3a_0 - a_1)T^2] \\ a_4 = \frac{1}{2T^4}[-30h + (14v_1 + 16v_0)T + (3a_0 - 2a_1)T^2] \\ a_5 = \frac{1}{2T^5}[12h - 6(v_1 + v_0)T + (a_1 - a_0)T^2] \end{cases} $$
对于具有 $n$ 个数据点的情况,可以对所有相邻的2个点应用上述公式,最终得到最终的插值曲线。