• 1. 梯度下降 / Gradient Descent
  • 1.1. 罗尔中值定理 / Rolle’s Mean Value theorem
  • 1.2. 拉格朗日中值定理 / Lagrange’s Mean Value Theorem
  • 1.3. 柯西中值定理 / Cauchy’s Mean Value Theorem
  • 1.4. 泰勒多项式 / Taylor Polynomials
  • 1.5. 梯度下降法 / Gradient Descent
• 2. 交叉熵 / Cross Entropy
  • 2.1. 信息熵 / Quantities of Information
  • 2.2. 相对熵 / Relative Entropy
  • 2.3. 交叉熵 / Cross Entropy
• 3. 非负矩阵分解 / Nonnegative Matrix Factorization (NMF) 「待补充更新」
  • 3.1. 标准方法
  • 3.2. 乘法更新法
• 4. TF-IDF
• 5. 正态分布 / Normal Distribution
• 6. Z-score
• 7. Sigmoid
• 8. Population Pearson Correlation Coefficient
• 9. Cosine Similarity
• 10. Naive Bayes
• 11. Maximum Likelihood Estimation (MLE)
• 12. Ordinary Least Squares (OLS)
• 13. F1 Score
• 14. 百分位数 / Quantile

1. 梯度下降 / Gradient Descent

梯度下降是一种无约束数学优化方法。它是一种一阶迭代算法，用于寻找可微分多元函数的局部最小值。要解释梯度下降算法就要首先了解三大微分中值定理（Mean Value Theorem）以及泰勒多项式（Taylor Polynomials）。

1.1. 罗尔中值定理 / Rolle’s Mean Value theorem

描述:

在实数域 $R$ 上的函数 $f(x)$ 满足：

1. 在闭区间 $[a,b]$ 上连续，
2. 在开区间 $(a,b)$ 内可导，
3. $f(a) = f(b)$，

则至少存在一个数 $\xi \in (a,b)$ 使得 $f'(\xi) = 0$。

证明:

因为 $f(x)$ 在 $[a,b]$ 上连续，所以存在最大值 $f_{max}$ 与 最小值 $f_{min}$，有以下两种情况：

1. 若 $f_{max} = f_{min}$，则 $f(x)$ 在 $[a,b]$ 上必为常函数，结论显然成立。
2. 若 $f_{max} > f_{min}$，因为 $f(a) = f(b)$，所以 $f(x)$ 在 $(a,b)$ 内至少有一个极值点。根据费马引理：可导函数极值点为 0 可推得，必存在某一点 $\xi$ 使得 $f'(\xi) = 0$

1.2. 拉格朗日中值定理 / Lagrange’s Mean Value Theorem

拉格朗日中值定理为罗尔中值定理的推广，同时也是柯西中值定理的特殊情形。

描述:

在实数域 $R$ 上的函数 $f(x)$ 满足：

1. 在闭区间 $[a,b]$ 上连续，
2. 在开区间 $(a,b)$ 内可导，

则至少存在一个数 $\varepsilon \in (a,b)$ 使得 $f'(\varepsilon) = \frac{f(b)-f(a)}{b-a}$ 成立。

证明:

即 $H(a) = H(b)$。根据罗尔中值定理 $\exists \xi \in (a,b)$ 使得 $H'(\xi) = f'(\xi) - \frac{f(b)-f(a)}{b-a} = 0$，即 $f'(\xi) = \frac{f(b)-f(a)}{b-a}$。

1.3. 柯西中值定理 / Cauchy’s Mean Value Theorem

描述:

在实数域 $R$ 上的函数 $f(x)$ 和 $g(x)$ 满足：

1. 在闭区间 $[a,b]$ 上连续，
2. 在开区间 $(a,b)$ 内可导，
3. $\forall x \in (a,b),\ g'(x) \neq 0$，

则至少存在一个数 $\psi \in (a,b)$ 使得 $\frac{f'(\psi)}{g'(\psi)} = \frac{f(b)-f(a)}{g(b)-g(a)}$ 成立。

证明:

1. 如果 $g(a) = g(b)$，由罗尔中值定理可得存在一点 $x_0 \in (a,b)$ 使得 $g'(x_0) = 0$，则与条件 3 矛盾，所以 $g(a) \neq g(b)$。
2. 假设存在函数 $H(x) = f(x) - \frac{f(b)-f(a)}{g(b)-g(a)} g(x)$，显然 $H(x)$ 在 $[a,b]$ 上连续且在 $(a,b)$ 内可导，同时有以下推证：

即 $H(a) = H(b)$，根据罗尔中值定理即证柯西中值定理。

1.4. 泰勒多项式 / Taylor Polynomials

首先，考虑一个函数 $f(x)$，它在 $x_0$ 处具有 $n+1$ 阶导数。泰勒公式的推导过程如下：

其中，$\varepsilon$ 位于 $x_0$ 和 $x$ 之间。

其中，$d$ 位于 $x_0$ 和 $\varepsilon$ 之间。将 $f'(\varepsilon)$ 的表达式代入第一步的等式中，得到： $f(x) - f(x_0) = f'(x_0)(x - x_0) + f''(d)\frac{(x - x_0)^2}{2}$

其中，$\varepsilon$ 位于 $x_0$ 和 $x$ 之间。

1.5. 梯度下降法 / Gradient Descent

梯度下降法是一种用于寻找函数局部最小值的优化算法，求解的是函数局部最小值所对应的解（即 $x$ 值）。其中 $x_{j+1}$ 和 $x_{j}$ 为迭代值，$\alpha$ 为步长。

有效性推导：

由于 ${f'(x_j)}^2 > 0$ 且 $\alpha > 0$，所以利用梯度下降法迭代的函数值一定是减小的。

2. 交叉熵 / Cross Entropy

信息熵由克劳德·艾尔肯·香农在1948年提出，用于描述信源输出符号的不确定度，即信源所含信息量的多少。在信息论中，信息熵表示了信息的混乱程度或无序度。简单来说，一个事件或一个系统（准确地说是一个随机变量）具有一定的不确定性，而信息熵就是衡量这种不确定性的度量。

2.1. 信息熵 / Quantities of Information

信息论中的信息量是一个抽象但至关重要的概念，它直观上可以理解为消除不确定性的度量。小概率事件的信息量大，大概率事件的信息量小。举个例子：“出门碰见人”这个高概率事件能给我们的信息就很少，几乎不包含有用的信息；但是“出门碰见外星人”这个极小概率事件的发生能给我们的信息就很多，因此信息量与事件概率是成反比的。

其中 $a=2$ 时信息量的单位是 bit，$a=e$ 时单位是 nit，$a=10$ 时单位是 hart。

其中 $X$ 为消息，$p(x_i)$ 为消息中的字符出现的统计学概率。上述平均信息量的公式与热力学和统计学中关于系统熵的公式一致，因此平均信息量也叫做信源的熵，即信息熵。

举例：
假设一离散信源发出由 0，1，2，3 四个字符组成的信息，他们统计学上的概率为 $\frac{3}{8}$，$\frac{1}{4}$，$\frac{1}{4}$，$\frac{1}{8}$；消息序列包含 57 个字符，0 出现 23 次，1 出现 14 次，2 出现 13 次，3 出现 7 次。

2.2. 相对熵 / Relative Entropy

KL 散度越小两个分布之间越接近。

2.3. 交叉熵 / Cross Entropy

3. 非负矩阵分解 / Nonnegative Matrix Factorization (NMF) 「待补充更新」

非负矩阵分解(Nonnegative Matrix Factorization),简称NMF,是由Lee和Seung于1999年在自然杂志上提出的一种矩阵分解。它使分解后的所有分量均为非负值(要求纯加性的描述)并且同时实现非线性的维数约减。

非负矩阵分解将一个矩阵 $V$ 近似分解成两个非负的矩阵 $W$ 和 $H$，即$V \approx W \times H$，其中$W,H \geq 0$。那么利用迭代优化的思想使得 $W \times H$ 的结果尽可能接近$V$，有

其中$s.t.$（subject to）为“受限于，服从于”的意思。

3.1. 标准方法

3.2. 乘法更新法

4. TF-IDF

TF-IDF（Term Frequency-Inverse Document Frequency）常用于信息检索。如果某个词在一片文章中出现的频率越高，该词所包含的信息就越多；如果该词在语料库中出现在不同文章的频率越高，该词所包含的信息就越少。该算法可以概括如下：

5. 正态分布 / Normal Distribution

正态分布（物理学中通称，高斯分布）是实值随机变量的一种连续概率分布，其概率密度函数 $f(x | \mu , \sigma^2)$ 为

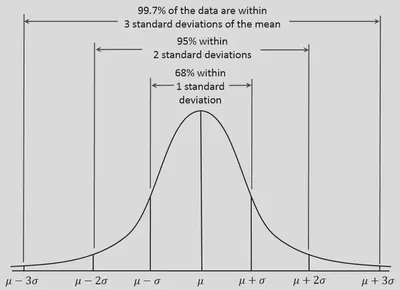
正态分布有如下图所示规律：在距平均值小于一个标准差、二个标准差、三个标准差以内的较精确百分比是68.27%、95.45%及99.73%。在实验科学中有对应正态分布的三西格马法则（three-sigma rule of thumb）：“几乎所有”的值都在平均值正负三个标准差的范围内，也就是在实验上可以将99.7%的概率视为“几乎一定”。但具体标准还要视情况讨论。

6. Z-score

In statistics, the standard score (Z-score) is the number of standard deviations by which the value of a raw score (i.e., an observed value or data point) is above or below the mean value of what is being observed or measured. Raw scores above the mean have positive standard scores, while those below the mean have negative standard scores.

7. Sigmoid

Sigmoid function is any mathematical function whose graph has a characteristic S-shaped or sigmoid curve. A common example of a sigmoid function is the logistic function shown below.

8. Population Pearson Correlation Coefficient

In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1.

9. Cosine Similarity

10. Naive Bayes

11. Maximum Likelihood Estimation (MLE)

12. Ordinary Least Squares (OLS)

13. F1 Score

14. 百分位数 / Quantile

分位数，也称分位点。此处展示的分位数算法以 python 中的 numpy 依赖包为参考。

1. 对于某一数据序列 $X$，我们首先对序列进行升序排序得到排序后的序列 $X_{sorted}$。

2. $$ i = q \times (\mathsf{lenth}(X_{sorted})-1) $$

   其中，$q$ 是所求分位数（第一百分位数即q=0.01，第九十九百分位数即q=0.99）.

3. $$ \mathsf{Quantile} = (1-\alpha) \times X_{\left\lfloor i\right\rfloor} + \alpha \times X_{\left\lceil i\right\rceil} \\ \alpha = i - \left\lfloor i\right\rfloor $$

   其中，$\left\lfloor i\right\rfloor$ 和 $\left\lceil i\right\rceil$ 分别表示 $i$ 的向下和向上取整。

参考代码：

import numpy as np
actions = [-0.41691166162490845,0.656757,0.41691166162490845]
# actions = [1,10]
actions_sort = sorted(actions) # 先进行排序
quantiles = 0.01 # 百分位

q01 = np.quantile(actions, quantiles, axis=0).tolist()
print(q01)

n = len(actions_sort)
i = quantiles * (n-1)
alph = i-round(i)
q02 = (1-alph)*actions_sort[round(i)] + alph*actions_sort[round(i)+1]
print(q02)