参考文献：

1. 大规模语言模型：从理论到实践
2. 一文看懂 LLaMA 中的旋转式位置编码（Rotary Position Embedding）

LLaMA 所采用的 Transformer 结构和细节与原始Transformer 架构不同的地方包括：

• 采用了前置层归一化（Pre-normalization）
• 使用 RMSNorm 归一化函数 （Normalizing Function）
• 激活函数更换为 SwiGLU
• 使用了旋转位置嵌入（RoP）

其整体架构与 GPT-2 类似，GPT-2模型架构如下图所示

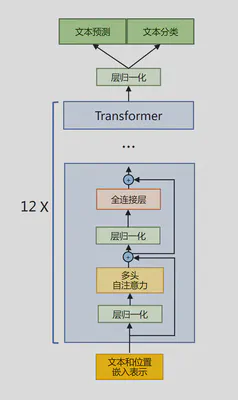
为了使得模型训练过程更加稳定，GPT-2 相较于 GPT 引入了前置层归一化方法，将第一个层归一化移动到多头自注意力层之前，第二个层归一化也移动到了全连接层之前；同时残差连接的位置也调整到了多头自注意力层与全连接层之后。

RMSNorm 归一化函数

LLaMA层归一化中也采用了 RMSNorm 归一化函数。对于输入向量$a_i$，其归一化后的值$\bar{a}_i$为 $$ \bar{a}_i = \alpha \cdot \frac{a_i}{RMS(a)} + b_i $$

其中$RMS(a) = \sqrt{\frac{1}{n}\sum^n_{j=1}a_j^2}$，$\alpha$与$b_i$是可学习的参数。

SwiGLU 激活函数

SwiGLU 激活函数在 PaLM 等模型中广泛应用并且取得了不错的效果。在 LLaMA 中全连接层 使用带有 SwiGLU 激活函数的 FFN（Position-wise Feed-Forward Network）的计算公式如下： $$ \begin{align} &FFN_{SwiGLU}(x, W , V , W_2) = SwiGLU(x, W , V )W_2 \\ &SwiGLU(x, W , V ) = Swish_\beta(xW) \otimes xV \\ &Swish_\beta(x) = x \cdot \sigma(\beta x) \end{align} $$

其中，$\sigma(x)$是Sigmoid函数，$\otimes$表示逐元素相乘，$W,V$为可学习的参数。

当$\beta = 1$时即SiLU激活函数

GLU激活函数

SwiGLU 激活函数是GLU激活函数的变体，GLU激活函数的通用形式如下图所示 $$ GLU(x, W , V ) = \sigma(xW + b) \otimes (xV + c) $$

其中$\sigma(x)$可以使用其他函数替换，用以生成其他变体。

旋转位置嵌入（RoPE）

在位置编码上，使用旋转位置嵌入（Rotary Positional Embeddings，RoPE） 代替原有的绝对位置编码。RoPE 借助了复数的思想，出发点是通过绝对位置编码的方式实现相对位置编码。其目标是通过下述运算来给 $q,k$ 添加绝对位置信息：

首先设一长度为$N$的输入序列为： $$ S_N = \{w_i\}^N_{i=1} $$

其中$w_i$表示输入序列中第$i$个token，而输入序列$S_N$对应的词嵌入编码序列为： $$ E_N = \{x_i\}^N_{i=1} $$

其中$x_i$表示$w_i$所对应的词嵌入向量，$x_i$的维度为$d$。

在计算注意力得分之前，会先用词嵌入向量结合位置编码信息计算 $q, k, v$ 向量，函数公式表达如下： $$ \begin{align} &q_m = f_q(x_m,m) = W_q (x_m + p_m) \\ &k_n = f_k(x_n,n) = W_k (x_n + p_n) \\ &v_n = f_v(x_n,n) = W_v (x_n + p_n) \end{align} $$

其中 $q_m$ 表示第 $m$ 个 token 对应的词向量 $x_m$ 集成位置信息 $m$ 之后的 query 向量，而 $k_n$ 和 $v_n$ 则表示第 $n$ 个 token 对应的词向量 $x_n$ 集成位置信息 $n$ 之后的 key 和 value 向量；$f_q, f_k, f_v$ 分别对应于想应的映射关系。

而计算第 $m$ 个词嵌入向量 $x_m$ 对应的注意力得分就是 $q_m$ 和其他 $\{k_n\}^N_{n=1}$ 都计算一个score ，然后再将 score 乘以对应的 $v_n$ 再求和得到输出向量 $o_m$： $$ \begin{align} &s_{m,n} = \frac{e^{(\frac{q^\mathsf{T}_m k_n}{\sqrt{d}})}}{\sum^N_{j=1}e^{(\frac{q^\mathsf{T}_m k_j}{\sqrt{d}})}} = \mathsf{softmax}(\frac{q^\mathsf{T}_m k_n}{\sqrt{d}}) \\ &o_m = \sum^N_{n=1} \left( s_{m,n} \cdot v_n \right) \end{align} $$

相对位置编码

从上面所推导的式子可以看出，只有 $q^\mathsf{T}_m k_n$ 这里可以利用上相对位置信息。由此我们如果想利用上词之间的相对位置信息，就可以假设存在一个函数$g$，其可以表示 $q_m$ 与 $k_n$ 的内积， 即 $$ g(x_m, x_n, m-n) = $$

其中 $x_m$ 与 $x_n$ 为词向量，$m-n$ 为两两词在句子中的相对位置。

内积的数学符号"<>" 内积或点积的数学符号一般表示为 $\vec{a} \cdot \vec{b}$。如果在高维空间，通常用$<>$表示。$<\vec{a}, \vec{b}> = \sum a_i * b_i$。

接下来，我们就需要构造一个满足上述关系的 $g$ 函数。原论文提出如下思路： $$ \begin{align} &f_q(x_m,m) = (W_q x_m) e^{im\theta} \\ &f_k(x_n,n) = (W_k x_n) e^{in\theta} \\ &g(x_m, x_n, m-n) = Re[(W_q x_m)(W_k x_n)^* e^{i (m-n) \theta}] \end{align} $$

在三角函数位置编码中，$f_q(x_m,m) = W_q (x_m + p_m)$，$f_k(x_n,n) = W_k (x_n + p_n)$

根据欧拉公式有 $$ e^{ix} = \cos x + i \sin x $$

由此我们可得 $$ \begin{align} &e^{im\theta} = \cos (m\theta) + i \sin (m\theta) \\ &e^{in\theta} = \cos (n\theta) + i \sin (n\theta) \\ &e^{i (m-n) \theta} = \cos ((m-n) \theta) + i \sin ((m-n) \theta) \end{align} $$

现在，我们先考虑简单情况，即 $W_q$ 与 $x_m$ 的维度都为2，我们有 $$ q_m = \left(\begin{matrix}q^{(1)}_m\\q^{(2)}_m\end{matrix}\right) = W_q x_m = \left(\begin{matrix}W^{(11)}_q&W^{(12)}_q\\W^{(21)}_q&W^{(22)}_q\end{matrix}\right)\left(\begin{matrix}x^{(1)}_m\\x^{(2)}_m\end{matrix}\right) $$

接着，我们将 $q_m$ 看作复数的表达形式 $$ q_m = \left(\begin{matrix}q^{(1)}_m\\q^{(2)}_m\end{matrix}\right) = q^{(1)}_m + i q^{(2)}_m $$

于是我们便有 $$ \begin{aligned} f_q(x_m,m) &= (W_q x_m) e^{im\theta} = q_m e^{im\theta} \\ &= (q^{(1)}_m + i q^{(2)}_m)*(\cos (m\theta) + i \sin (m\theta)) \\ &= (q^{(1)}_m \cos (m\theta) - q^{(2)}_m \sin (m\theta)) + i(q^{(2)}_m \cos (m\theta) + q^{(1)}_m \sin (m\theta)) \end{aligned} $$

重新将上述结果用实数形式表示为 $$ \begin{aligned} f_q(x_m,m) &= (W_q x_m) e^{im\theta} = q_m e^{im\theta} \\ &= \left[ q^{(1)}_m \cos (m\theta) - q^{(2)}_m \sin (m\theta), q^{(2)}_m \cos (m\theta) + q^{(1)}_m \sin (m\theta) \right] \\ &=\left(\begin{matrix} \cos (m\theta) & - \sin (m\theta) \\ \sin (m\theta) & \cos (m\theta) \end{matrix}\right) \left(\begin{matrix}q^{(1)}_m\\q^{(2)}_m\end{matrix}\right) \end{aligned} $$

以上表达形式与旋转矩阵相同，故叫做旋转式位置编码。 同理可得 $$ \begin{aligned} f_k(x_n,n) &= (W_k x_n) e^{in\theta} = k_n e^{in\theta} \\ &= \left(\begin{matrix} \cos (n\theta) & - \sin (n\theta) \\ \sin (n\theta) & \cos (n\theta) \end{matrix}\right) \left(\begin{matrix}k^{(1)}_n\\k^{(2)}_n\end{matrix}\right) \end{aligned} $$

至此，我们开始证明等式成立。首先计算$g(x_m, x_n, m-n)$ $$ \begin{aligned} g(x_m, x_n, m-n) &= Re[(W_q x_m)(W_k x_n)^* e^{i (m-n) \theta}] \\ &= (q^{(1)}_m k^{(1)}_n + q^{(2)}_m k^{(2)}_n)\cos ((m-n) \theta) - (q^{(2)}_m k^{(1)}_n - q^{(1)}_m k^{(2)}_n)\sin ((m-n) \theta) \end{aligned} $$

其中 $Re[x]$ 表示一个复数 $x$ 的实部部分，而 $(W_k x_n)^*$ 则表示复数 $W_k x_n$ 的共轭。 $$ \begin{cases} W_q x_m = q_m = q^{(1)}_m + i q^{(2)}_m \\ W_k x_n = k_n = k^{(1)}_n + i k^{(2)}_n \\ (W_k x_n)^* = k_n^* = k^{(1)}_n - i k^{(2)}_n \\ e^{i (m-n) \theta} = \cos ((m-n) \theta) + i \sin ((m-n) \theta) \end{cases} $$

接下来计算$\left\langle\left. f_q(x_m,m), f_k(x_n,n) \right\rangle\right.$: $$ \begin{aligned} \left\langle\left. f_q(x_m,m), f_k(x_n,n) \right\rangle\right. = & q^{(1)}_m \cos (m\theta) k^{(1)}_n \cos (n\theta) - q^{(1)}_m \cos (m\theta) k^{(2)}_n \sin (n\theta) \\ &- q^{(2)}_m \sin (m\theta) k^{(1)}_n \cos (n\theta) + q^{(2)}_m \sin (m\theta) k^{(2)}_n \sin (n\theta) \\ &+ q^{(2)}_m \cos (m\theta) k^{(2)}_n \cos (n\theta) + q^{(2)}_m \cos (m\theta) k^{(1)}_n \sin (n\theta) \\ &+ q^{(1)}_m \sin (m\theta) k^{(2)}_n \cos (n\theta) + q^{(1)}_m \sin (m\theta) k^{(1)}_n \sin (n\theta) \end{aligned} $$

其中 $$ \begin{cases} f_q(x_m,m) = \left[ q^{(1)}_m \cos (m\theta) - q^{(2)}_m \sin (m\theta), q^{(2)}_m \cos (m\theta) + q^{(1)}_m \sin (m\theta) \right] \\ f_k(x_n,n) = \left[ k^{(1)}_n \cos (n\theta) - k^{(2)}_n \sin (n\theta), k^{(2)}_n \cos (n\theta) + k^{(1)}_n \sin (n\theta) \right] \end{cases} $$

根据三角函数性质化简后可得 $$ \begin{aligned} g(x_m, x_n, m-n) &= \left\langle\left. f_q(x_m,m), f_k(x_n,n) \right\rangle\right. \\ &= \left( \begin{matrix}q^{(1)}_m & q^{(2)}_m\end{matrix} \right) \left( \begin{matrix} \cos ((m-n))\theta) & - \sin ((m-n)\theta) \\ \sin ((m-n)\theta) & \cos ((m-n)\theta) \end{matrix} \right) \left( \begin{matrix} k^{(1)}_n \\ k^{(2)}_n \end{matrix} \right) \end{aligned} $$

以上是维度为2的形式。若维度大于2且可以被2整除，那么存在以下形式 $$ \theta_j = \theta_{j+1} = 10000^{-2(j-1)/d}, \ j \in [1, 2, ..., d/2] $$

更简单的证明

利用旋转矩阵的性质 假设 $R_a$ 表示角度为 $a$ 的旋转矩阵，那么 $R$ 具有如下性质： $$ \begin{align} &R(a)^\mathsf{T} = R(-a) \\ &R(a) \times R(b) = R(a+b) \end{align} $$

由此化简问题为证明 $\left\langle\left. R(a)X,R(b)Y \right\rangle\right. = \left\langle\left. X,R(b-a)Y \right\rangle\right.$ 成立，证明如下 $$ \begin{aligned} \left\langle\left. R(a)X,R(b)Y \right\rangle\right. &= (R(a)X)^\mathsf{T} \times R(b)Y \\ &= X^\mathsf{T} \times R(a)^\mathsf{T} \times R(b)Y \\ &= X^\mathsf{T} \times R(-a) \times R(b)Y \\ &= X^\mathsf{T} \times R(b-a) \times Y \\ &= \left\langle\left. X,R(b-a)Y \right\rangle\right. \end{aligned} $$

即证