Transformer 架构 / Transformer - LLM Architecture

4月 30, 2024·
Junhong Liu
Junhong Liu
· 8 分钟阅读时长

参考文章：

  1. The Illustrated Transformer
  2. The Illustrated Transformer（中文版）
  3. Glossary of Deep Learning: Word Embedding
  4. 从0开始词嵌入（Word embedding）
  5. GloVe: Global Vectors for Word Representation
  6. Efficient Estimation of Word Representations in Vector Space
  7. GloVe模型的原理与实现
  8. GloVe模型总结
  9. Layer Normalization

目录：

1. 词编码

使用Transformer模型的第一步就是将需要输入的词汇进行编码(Word Embedding)，其基本思想就是将字符串类型的文本数据，转换成数字类型的向量数据。

简单来说，词嵌入(Word Embedding)是一种从文本语料库构建低维向量表示的方法，它保留了单词的上下文语义相似性[3]。

1.1. 独热编码 / One-Hot Representation

假如我们要计算的文本中一共出现了4个词：猫、狗、牛、羊。我们使用向量里每一个位置来代表一个词。所以使用独热编码算法后的数据转化为：

$$ 猫：[1,0,0,0] \\ 狗：[0,1,0,0] \\ 牛：[0,0,1,0] \\ 羊：[0,0,0,1] $$ 
# 调用scikit-learn包
from sklearn.feature_extraction.text import CountVectorizer

def one_hot(texts):
    
    # CountVectorizer：文本特征提取计算类，会将文本中的词语转换为词频矩阵，它通过fit_transform函数计算各个词语出现的次数
    vectorizer = CountVectorizer(binary=True)
    texts = vectorizer.fit_transform(texts)  # 拟合模型，并返回文本矩阵
    print(vectorizer.get_feature_names_out())
    return texts

text = ['I hope you know, I love you','I hope you know', 'I love you']
text = one_hot(text)  # 此处text为csr_matrix类型，是一个稀疏矩阵。如：(2, 3)    1代表第二行第三列的值为1，其余全为0。
print(text)

输出：

['hope' 'know' 'love' 'you']
(0, 0)        1
(0, 3)        1
(0, 1)        1
(0, 2)        1
(1, 0)        1
(1, 3)        1
(1, 1)        1
(2, 3)        1
(2, 2)        1

缺点

  • 维度爆炸。由于每一个单词的词向量的维度都等于词汇表的长度，对于大规模语料训练的情况，词汇表将异常庞大，使模型的计算量剧增造成维数灾难。
  • 矩阵稀疏。有用的信息零散地分布在大量数据中。这会导致结果异常稀疏，使其难以进行优化，对于神经网络来说尤其如此。
  • 向量正交。由于两两向量正交，无法表达两词向量之间的其他信息，造成了“语义鸿沟”的现象，此特点对于NLP任务是相当致命的。

1.2. 词袋模型 / Bag of Words

词袋模型不考虑语法、词的顺序，只考虑所有的词的出现频率。向量的维度根据词典中不重复的词的个数确定，向量中每个元素顺序与原来文本中单词出现的顺序没有关系,向量中每个数字是词典中每个单词在文本中出现的频率。

# 调用scikit-learn包
from sklearn.feature_extraction.text import CountVectorizer

def bow(texts):

    # CountVectorizer：文本特征提取计算类，会将文本中的词语转换为词频矩阵，它通过fit_transform函数计算各个词语出现的次数

    vectorizer = CountVectorizer()
    texts = vectorizer.fit_transform(texts)  # 拟合模型，并返回文本矩阵
    print(vectorizer.get_feature_names_out())  # 获得所有文本的词汇；列表型
    return texts

text = ['I hope you know, I love you','I hope you know', 'I love you']
text = bow(text)  # 此处text为csr_matrix类型，是一个稀疏矩阵。如：(2, 3)   1代表第二行第三列的值为1，其余全为0。
print(text.toarray())  # 将csr_matrix转换为ndarray

输出：

['hope' 'know' 'love' 'you']
[[1 1 1 2]
[1 1 0 1]
[0 0 1 1]]

词袋模型与独热编码相比，多了词频信息。

1.3. N-gram模型

N-gram也是一种基于统计语言模型的算法。它的基本思想是将文本里面的内容按照字节进行大小为N的滑动窗口操作，形成了长度是N的字节片段序列。每一个字节片段称为gram，对所有gram的出现频度进行统计，并且按照事先设定好的阈值进行过滤，形成关键gram列表，也就是这个文本的向量特征空间，列表中的每一种gram就是一个特征向量维度。

该模型基于这样一种假设，第N个词的出现只与前面N-1个词相关，而与其它任何词都不相关，整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。当 N=1 时称为 unigram 模型即一元模型，也叫上下文无关模型，上文提到的词袋模型就是 unigram 模型；当 N=2 时称为 bigram 模型即二元模型；当 N=3 时称为 trigram 模型即三元模型。

from sklearn.feature_extraction.text import CountVectorizer

def n_gram(texts):
    
    # CountVectorizer：文本特征提取计算类，会将文本中的词语转换为词频矩阵，它通过fit_transform函数计算各个词语出现的次数
    vectorizer = CountVectorizer(ngram_range=(1,2)) # ngram_range参数：词组切分的长度范围
    texts = vectorizer.fit_transform(texts)  # 拟合模型，并返回文本矩阵
    print(vectorizer.get_feature_names_out())  # 获得所有文本的词汇；列表型
    return texts

text = ["I hope you know, I love you",'I hope you know', 'I love you']
text = n_gram(text)  # 此处text为csr_matrix类型，是一个稀疏矩阵。如：(2, 3)   1代表第二行第三列的值为1，其余全为0。
print(text.toarray())  # 将csr_matrix转换为ndarray

输出：

['hope' 'hope you' 'know' 'know love' 'love' 'love you' 'you' 'you know']
[[1 1 1 1 1 1 2 1]
[1 1 1 0 0 0 1 1]
[0 0 0 0 1 1 1 0]]

N-gram 模型的基本原理是基于马尔可夫假设，在训练 N-gram 模型时使用最大似然估计模型参数——条件概率。当N更大的时候，对下一个词出现的约束性信息更多，有更大的辨别力，但是更稀疏，并且N-gram的总数也更少；当N更小的时候，在训练语料库中出现的次数更多，有更可靠的统计结果，更高的可靠性 ，但是约束信息更少。并且 N-gram 模型无法避免零概率问题（当某个输入词语未出现在语料库中时，会导致整个语句的概率为0），导致无法获得良好的语言模型。

1.4. 词频-逆文档模型 / TF-IDF模型

前文提到的几种方法都是基于单词在文档中出现的频率来判断来猜测语义，也符合人类对于语言的理解规律。可是，出现频率越大的词往往对于判断语义并没有实质性的帮助，例如“我”，“是”，“的”，“今天”等词语。而像“足球”，“口红”，“股票”等词则更能反应一篇文章的主题。

为了解决这个问题，我们提出两种解决方案：第一个是增加停用词（stop word），通过自定义词典，来去掉一些无用的高频词；第二个就是 TF-IDF 模型。

TF-IDF算法是一种可应用于多个领域的加权技术，它是基于统计的方法，根据某关键字或词在文档或语料集中出现的频率来估计它对于文件的重要程度。TF-IDF算法常常被用于信息检索任务中。算法的核心思想是，字词在文档中出现的次数越多，其重要程度就越高，但它如果在语料集出现的次数越多，它的重要程度则会随之降低。

TF（Term Frequancy）代表词频，表示词在文档中出现的频率。IDF（Inverse Document Frequency）代表逆文档频率。TF-IDF值越高，则表示此词在一篇文档中出现概率高并且在其他文档中出现概率低，说明这个词具有良好的类别区分能力，应赋予其更高的权重。 $$ TF-IDF = TF \times IDF $$ $$ TF = \frac{某词在文档中出现的次数}{文档的总词量} $$ $$ IDF = \ln \left( \frac{语料库中文档总数}{包含该词的文档数+1} \right) $$ 

from sklearn.feature_extraction.text import TfidfVectorizer

def tfidf(texts):
   
    # CountVectorizer：文本特征提取计算类，会将文本中的词语转换为词频矩阵，它通过fit_transform函数计算各个词语出现的次数
   
    vectorizer = TfidfVectorizer(ngram_range=(1, 2))
    texts = vectorizer.fit_transform(texts)  # 拟合模型，并返回文本矩阵
    print(vectorizer.get_feature_names_out())  # 获得所有文本的词汇；列表型
    return texts

text = ["I hope you know, I love you",'I hope you know', 'I love you']
text = tfidf(text)  # 此处text为csr_matrix类型，是一个稀疏矩阵。如：(2, 3)   1代表第二行第三列的值为1，其余全为0。
print(text)

输出：

['hope' 'hope you' 'know' 'know love' 'love' 'love you' 'you' 'you know']
(0, 5)        0.3140174490783707
(0, 3)        0.412895209095628
(0, 7)        0.3140174490783707
(0, 1)        0.3140174490783707
(0, 4)        0.3140174490783707
(0, 2)        0.3140174490783707
(0, 6)        0.4877251237651747
(0, 0)        0.3140174490783707
(1, 7)        0.46609584262774545
(1, 1)        0.46609584262774545
(1, 2)        0.46609584262774545
(1, 6)        0.3619650009883935
(1, 0)        0.46609584262774545
(2, 5)        0.6198053799406072
(2, 4)        0.6198053799406072
(2, 6)        0.48133416873660545

1.5. Word2Vec 模型

2013年，Google 团队提出了开源的训练词嵌入向量的工具Word2vec，它的核心思想是根据关键词去预测其上下文或根据上下文去预测关键词。 Word2vec 词嵌入模型能够很好的表示词与词之间的类比关系和相似关系。Word2vec 模型包含两种结构：CBOW、skip-gram；和两种优化方法softmax、negative sampling。

1.5.1. CBOW 模型

CBOW(continuous bag of words)模型的核心思想是：在一个句子中遮住目标单词，通过其前面以及后面的单词来推测出这个单词w。首先规定词向量的维度V，对数据中所有的词随机赋值为一个V维的向量，每个词向量乘以参数矩阵W(VN维矩阵)，转换成N维数据，然后要对窗口范围内上下文的词向量相加取均值作为输入层输入到隐藏层，隐藏层将维度拉伸后全连接至输出层然后做一个softmax的分类从而预测目标词。最终用预测出的w与真实的w作比较计算误差函数，然后用梯度下降调整参数矩阵。

1.5.2. skip-gram 模型

skip-gram模型的核心思想是：模型根据目标单词来推测出其前面以及后面的单词。它的模型结构与CBOW正好相反，只不过它的输入是目标词，输出是目标词的邻接词，从模型结构示意图上看相当于输入层与输出层交换位置，先将目标词词向量映射到投影层，再将投影层的输出作为输出层的输入，最后预测目标词窗口范围内的邻接词。

Word2Vec 的缺点是，由于其训练出来的词嵌入向量表示与单词是一对一的关系，一词多义问题还是没有解决。单词在不同上下文中是具有不一样含义的，而 Word2Vec 学习出来的词嵌入表示不能考虑不同上下文的情况。

1.6. GloVe 模型

GloVe模型于2014年被提出。上文讲的 Word2vec模型只考虑到了词与窗口范围内邻接词的局部信息，没有考虑到词与窗口外的词的信息，没有使用语料库中的统计信息等全局信息，具有局限性。GloVe模型则使用了考虑全局信息的共现矩阵和特殊的损失函数，有效解决了 Word2vec的部分缺点。

1.6.1. 共现矩阵

设

  • word-word共现矩阵（matrix of word-word co-occurrence counts）: $X$
  • 词$j$出现在词$i$上下文的次数: $X_{ij}$

我们有 $$ X_i=\sum^{j \in K} X_{ij} \\ P_{ij}=P(j|i)=X_{ij}/X_i $$

其中$X_i$表示出现在词$i$上下文的所有词的次数总和，$K$表示所有词的集合，$P_{ij}$表示词$j$出现在词$i$上下文窗口中的概率。

举例：

Probability and Ratio $k = solid$ $k = gas$ $k = water$ $k = fashion$
$P(k\|ice)$ $1.9 \times 10^{−4}$ $6.6 \times 10^{−5}$ $3.0 \times 10^{−3}$ $1.7 \times 10^{−5}$
$P(k\|steam)$ $2.2 \times 10^{−5}$ $7.8 \times 10^{−4}$ $2.2 \times 10^{−3}$ $1.8 \times 10^{−5}$
$P(k\|ice)/P(k\|steam)$ $8.9$ $8.5 \times 10^{-2}$ $1.36$ $0.96$

假设$i=ice$，$j=steam$，这两个单词的关系可以通过学习它们分别与第三个词的共现概率的比率来表示。如果$k=solid$，那么$k$与$i$更加相关，因此我们希望$P_{ik}/P_{jk}$的值比较大。同样的，$k=gas$，那么$k$与$j$更加相关，因此我们希望$P_{ik}/P_{jk}$的值很小。那么对于$k=water$或者$fashion$，$k$同时与$i$和$j$相关或不相关，此时$P_{ik}/P_{jk}$的值接近1。即有如下规律

$P(k\|ice)/P(k\|steam)$ $j,k$相关 $j,k$不相关
$i,k$相关 趋近1 较大
$i,k$不相关 较小 趋近1

综上所述，$\frac{P_{ik}}{P_{jk}}$与词$i,j,k$相关,由此我们假设存在函数$F$，使得 $$ F(w_i,w_j,\widetilde{w}_k) = \frac{P_{ik}}{P_{jk}} $$

其中 $w \in \mathbb{R}^d$ ，$\widetilde{w} \in \mathbb{R}^d$ 为词向量。

为了表示词向量在向量空间中的线性关系，这里使用差分的形式进行表示： $$ F((w_i-w_j),\widetilde{w}_k) = \frac{P_{ik}}{P_{jk}} $$

其中，左边参数为向量，右边为标量，我们可以使用比较复杂的神经网络来实现这个$F$函数，但是神经网络会把我们试图获取到的线性关系抵消掉。因此，使用向量点乘的方式来表示左边的参数： $$ F((w_i-w_j)^\mathsf{T}\widetilde{w}_k) = \frac{P_{ik}}{P_{jk}} $$

至此，我们需要构造一个函数$F$使得上述等式成立。令 $$ F((w_i-w_j)^\mathsf{T}\widetilde{w}_k) = F(w_i^\mathsf{T}\widetilde{w}_k - w_j^\mathsf{T}\widetilde{w}_k) = \frac{F(w_i^\mathsf{T}\widetilde{w}_k)}{F(w_j^\mathsf{T}\widetilde{w}_k)} = \frac{P_{ik}}{P_{jk}} $$

可推得$F(x) = e^x$，且 $F(w_i^\mathsf{T}\widetilde{w}_k) = P_{ik}$ ，同理 $F(w_j^\mathsf{T}\widetilde{w}_k) = P_{jk}$ 。

由此我们有 $$ w_i^\mathsf{T}\widetilde{w}_k = \ln{P_{ik}} = \ln{\frac{X_{ik}}{X_i}} = \ln X_{ik} - \ln X_i $$

即 $w_i^\mathsf{T}\widetilde{w}_k + \ln X_i = \ln X_{ik}$ ，加上偏执项后得 $w_i^\mathsf{T}\widetilde{w}_k + \ln X_i + b_i + \widetilde{b}_k = \ln X_{ik}$ 。由于$\ln X_i$是一个只与词$i$有关得常量，所以简化进$i$得偏执$b_i$中。最终式为 $$ w_i^\mathsf{T}\widetilde{w}_k + b_i + \widetilde{b}_k = \ln X_{ik} $$

由此我们使用平方差损失函数来构建目标函数 $$ J = \sum^{i,j \in K}(w_i^\mathsf{T}\widetilde{w}_j + b_i + \widetilde{b}_j - \ln X_{ij})^2 $$

此外，为了减小出现频率较小(可能是噪声)或较大的词的权重。这里在上述目标函数的基础上引入权重$f(X_{ij})$，有 $$ f(x) = \begin{cases} (x/x_{max})^\alpha,& \mathsf{if}\ x < x_{max} \\ 1,& \mathsf{otherwise}. \end{cases} $$

其中，$x_{max}$在原论文中固定为$100$，$\alpha$在原论文中设置为$3/4$。

2. Transformer结构

Transformer模型总体上看由编码模块、解码模块及它们之间的连接层组成。输入数据先通过编码模块进行编码，随后通过解码模块得到输出信息。

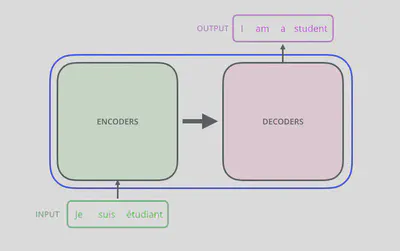
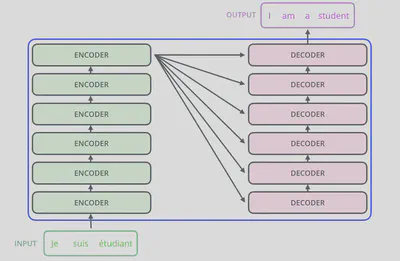
The_transformer_encoders_decoders

编码模块由六层编码器(Encoder)构成，解码模块同样由六层解码器(Decoder)构成。每个编码器与解码器的结构完全相同，但并不共享参数。

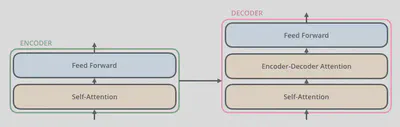
The_transformer_encoders_decoders

其中编码器与解码器的结构如下图所示。编码器由一个自注意力层(Self-attention)和一个前馈网络层(Feed Forward)组成，解码器由两个自注意力层(注意，这两个自注意力层并不完全相同)和一个前馈网络层组成。

The_transformer_encoders_decoders

3. 位置编码

参考文章：

  1. Transformer Architecture: The Positional Encoding
  2. Transformer Architecture: The Positional Encoding（中文版）
  3. Reddit thread - Positional Encoding in Transformer
  4. 证明高维空间随机取两个向量几乎正交
  5. 位置编码可视化示意图
  6. 《Attention Is All You Need》

理想的位置编码应满足以下条件[1]：

  • 每个时间步都有唯一的编码
  • 相邻两个时间步之间的距离应该一致，且不受句子长度的影响
  • 编码后的值得范围是有界，且确定的

3.1. 三角函数位置编码

《Attention Is All You Need》中提出一种利用三角函数的编码方式。三角函数位置编码不再使用单独某个数字，而是使用一个$d$维向量来表示位置。

首先，设

  • $l \in (0,1,2,3...,n-1)$。
  • $mod(d,2) = 0$。
  • $\vec{P_l} \in \mathbb{R}^d$。

其中$l$为某个词汇在句子中的位置，$n$为句子所包含的词汇量，$d$为位置编码向量的维度，$P$为位置编码向量所组成的矩阵，$\vec{P_l}$为位置$l$的位置编码向量，$\vec{P_l^i}$为位置编码向量$\vec{P_l}$的第$i$维的值（即第$i$个元素的值）。

对于$\vec{P_l^i}$，我们有 $$ \vec{P_l^i} = \begin{cases} \sin(w_k \cdot l),& \mathsf{if}\ i = 2k \\ \cos(w_k \cdot l),& \mathsf{if}\ i = 2k+1. \end{cases} $$ $$ w_k = \frac{1}{10000^{(2k/d)}} $$

由此便可以得到词汇的位置编码 $$ \vec{P_l} = [\sin(w_1 \cdot l), \cos(w_1 \cdot l), ..., \sin(w_{d/2} \cdot l), \cos(w_{d/2} \cdot l)] \in \mathbb{R}^d $$

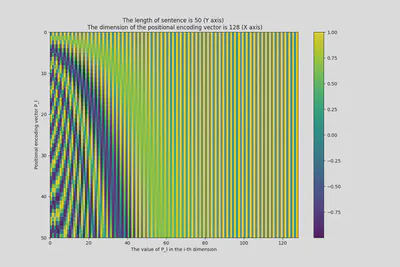
其可视化[5]如下图所示:

positional_encoding

可视化代码

import numpy as np
import matplotlib.pyplot as plt
     
## 编码算法
# Code from https://www.tensorflow.org/tutorials/text/transformer
def get_angles(pos, i, d_model):
  angle_rates = 1 / np.power(10000, (2 * (i//2)) / np.float32(d_model))
  return pos * angle_rates

def positional_encoding(position, d_model):
  angle_rads = get_angles(np.arange(position)[:, np.newaxis],
                          np.arange(d_model)[np.newaxis, :],
                          d_model)
  
  # apply sin to even indices in the array; 2i
  angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])
  
  # apply cos to odd indices in the array; 2i+1
  angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])
    
  pos_encoding = angle_rads[np.newaxis, ...]
    
  return pos_encoding

## 可视化
tokens = 50
dimensions = 128

pos_encoding = positional_encoding(tokens, dimensions)
print (pos_encoding.shape)

plt.figure(figsize=(12,8))
plt.pcolormesh(pos_encoding[0], cmap='viridis')
plt.xlabel('The value of P_l in the i-th dimension')
plt.xlim((0, dimensions))
plt.ylim((tokens,0))
plt.ylabel('Positional encoding vector P_l')
plt.title('The length of sentence is 50 (Y axis) \n The dimension of the positional encoding vector is 128 (X axis)')
plt.colorbar()
plt.show()

3.1.1. 嵌入位置编码

为了将位置编码信息嵌入到词编码中。原文[6]直接将位置编码与词编码相加，即对于某个句子$S_i$中的某个词汇$W_l$的编码$\Psi(W_l)$，其最终的编码为$\Psi'_l = \Psi(W_l) + \vec{P_l}$，显然$\vec{P_l}, \Psi(W_l) \in \mathbb{R}^d$。

3.1.2. 相对位置

采用三角函数编码的另一个特质是：可以计算两个词汇之间的相对位置。

设存在矩阵$M \in \mathbb{R}^{2 \times 2}$，使下面等式成立： $$ M \cdot \left[ \begin{matrix} \sin(w_k \cdot l) \\ \cos(w_k \cdot l) \end{matrix} \right] = \left[ \begin{matrix} \sin(w_k \cdot (l + \theta)) \\ \cos(w_k \cdot (l + \theta)) \end{matrix} \right] $$

我们有 $$ \begin{aligned} M \cdot \left[ \begin{matrix} \sin(w_k \cdot l) \\ \cos(w_k \cdot l) \end{matrix} \right] &= \left[ \begin{matrix} \sin(w_k \cdot l) \cos(w_k \cdot \theta) + \cos(w_k \cdot l) \sin(w_k \cdot \theta) \\ \cos(w_k \cdot l) \cos(w_k \cdot \theta) - \sin(w_k \cdot l) \sin(w_k \cdot \theta) \end{matrix} \right] \\ \left[ \begin{matrix} m_{11} & m_{12} \\ m_{21} & m_{22} \end{matrix} \right] \cdot \left[ \begin{matrix} \sin(w_k \cdot l) \\ \cos(w_k \cdot l) \end{matrix} \right] &= \left[ \begin{matrix} \sin(w_k \cdot l) \cos(w_k \cdot \theta) + \cos(w_k \cdot l) \sin(w_k \cdot \theta) \\ \cos(w_k \cdot l) \cos(w_k \cdot \theta) - \sin(w_k \cdot l) \sin(w_k \cdot \theta) \end{matrix} \right] \\ \left[ \begin{matrix} m_{11}\sin(w_k \cdot l)+m_{12}\cos(w_k \cdot l) \\ m_{21}\sin(w_k \cdot l)+m_{22}\cos(w_k \cdot l) \end{matrix} \right] &= \left[ \begin{matrix} \sin(w_k \cdot l) \cos(w_k \cdot \theta) + \cos(w_k \cdot l) \sin(w_k \cdot \theta) \\ \cos(w_k \cdot l) \cos(w_k \cdot \theta) - \sin(w_k \cdot l) \sin(w_k \cdot \theta) \end{matrix} \right] \end{aligned} $$

由此可得 $$ \begin{aligned} m_{11} &= \cos(w_k \cdot \theta) \\ m_{12} &= \sin(w_k \cdot \theta) \\ m_{21} &= -\sin(w_k \cdot \theta) \\ m_{22} &= \cos(w_k \cdot \theta) \end{aligned} $$

即 $$ M = \left[ \begin{matrix} \cos(w_k \cdot \theta) & \sin(w_k \cdot \theta) \\ -\sin(w_k \cdot \theta) & \cos(w_k \cdot \theta) \end{matrix} \right] $$

3.2. 为何位置编码使用嵌入而不是拼接

通过Reddit上用户[3]的回答，其提出假设：高维随机选择的向量几乎总是近似正交的，没有理由认为词编码向量和位置编码向量以任何方式相关。

如果为真，这将解释为什么嵌入位置编码是没问题。拼接位置编码将确保位置维度与单词维度正交，但如果位置编码与词编码的维度足够高，那么即使是将位置编码嵌入到词编码中也可以获得近似正交的特性。这样就节约了学习成本（需要学习更多参数，或添加更多的网络层）。

其中，知乎上的用户似乎提出证明：高维空间随机取两个向量几乎正交[4]。

4. 编码器

假设一个句子中得所有词的集合为$S$，则有词向量$\vec{x}_i \in S$且$\vec{x}_i \in \R^d$，其中$d$为词向量的维度（原论文中词向量的维度为512）。

embeddings

最开始，每个编码器都会接受一个词向量列表$L$作为输入，后一编码器接受前一编码器的输出。列表$L$的大小是可以设置的超参数，通常将其设置为训练集中最长句子的长度，其元素为词向量，即$L = [\vec{x}_1, \vec{x}_2, \vec{x}_3, ..., \vec{x}_n]$，其中$n$为最长句子的长度。

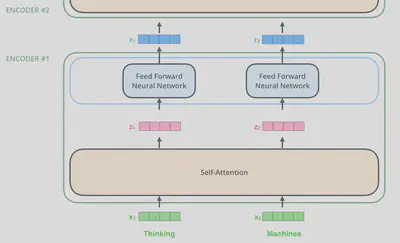
encoder_with_tensors_2

在self-attention层中，数据流会相互依赖/影响，但在前馈层中数据是独立处理的。

Self-attention机制的简单理解

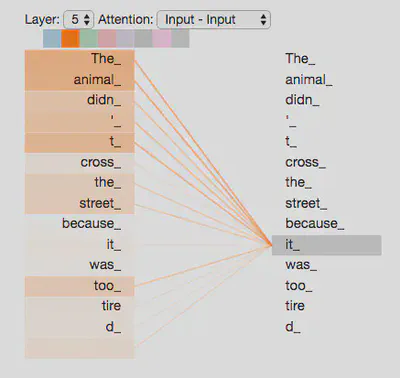
以如下句子为例:“The animal didn’t cross the street because it was too tired”。句子中“it”指的是“street”还是“animal”？此时self-attention机制允许模型在处理“it”的时候将其与“animal”联系起来。

当模型处理每个词的时候，self-attention机制允许模型将其与其他位置的词联系起来。

transformer_self_attention_visualization

4.1. Self-attention算法细节

4.1.1. 步骤1

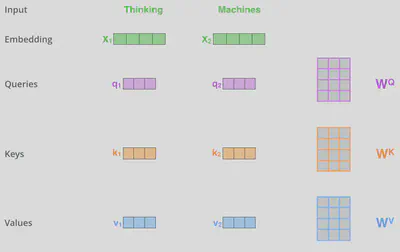
对于每个输入的词向量，都会通过三个可学习/训练的转换矩阵将其转换成三个不同的向量$\vec{q}$(query),$\vec{k}$(key),$\vec{v}$(value)。在原论文中，向量$\vec{q}, \vec{k}, \vec{v}$的维度（64）要小于词向量的维度（512），这并不是必须的，其目的是为了让self-attention的计算更稳定。维度的确定可以服从公式$d_q = d_k = d_v = d/h$，其中$d_q, d_k, d_v$分别为向量$\vec{q}, \vec{k}, \vec{v}$的维度，$h$为自注意力平行层的层数。

transformer_self_attention_vectors

4.1.2. 步骤2

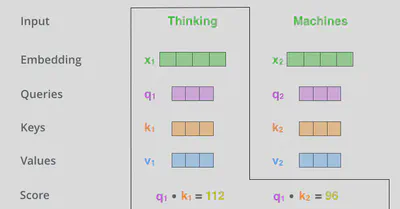
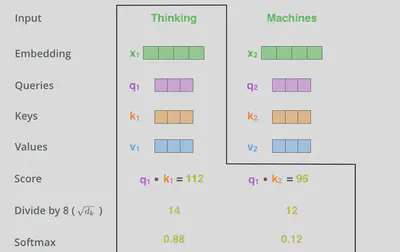
计算attention得分。对于“Thinking Matchines”这句话，在计算“Thinking”这个词的attention得分时，需要使用到其他词向量的信息。

设“Thinking”的词向量为 $\vec{x}_1$ ，“Matchines”的词向量为 $\vec{x}_2$ 。先计算 $Score$ 分数，其为 $\vec{q}$ 与 $\vec{k}$ 的点积。 $$ S_{ij} = \vec{q}_i \cdot \vec{k}_j $$

其中，$S_{ij}$为词向量$\vec{x}_i$与$\vec{x}_j$的$Score$分数，$\vec{x}_i, \vec{x}_j \in K$（$i$可以等于$j$），$K$为训练集中所有词向量的集合，$\vec{q}_i$为$\vec{x}_i$的query值，$\vec{k}_j$为$\vec{x}_j$的key值。

transformer_self_attention_score

4.1.3. 步骤3

将$S_{ij}$乘与$\frac{1}{\sqrt{d_k}}$，这样梯度会更稳定。随后进行softmax操作，对结果进行归一化。softmax后的值可以理解为一种权重，即每个词的表达程度（关注度）。

self_attention_softmax

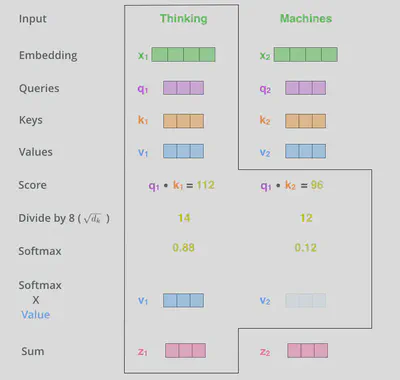
4.1.4. 步骤4

将softmax后的值与对应的词向量的$\vec{v}$相乘，随后将所有相乘后的加权$\vec{v}$相加，即attention得分。

self_attention_output

4.2. 利用矩阵快速计算Self-attention得分

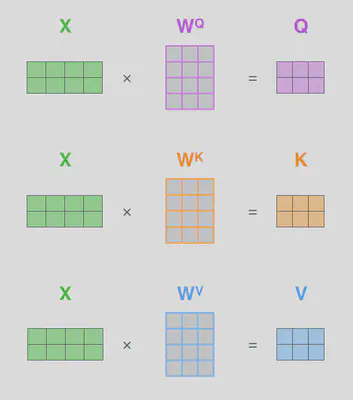
设

  • $X$为输入矩阵，$X \in \mathbb{R}^{n \times d}$，$n$为词向量的数量，$d$为词向量的维度。
  • $W^Q$为向量$\vec{q}$的转换矩阵，$W^Q \in \mathbb{R}^{d \times d_q}$，$d$为词向量的维度，$d_q$为向量$\vec{q}$的维度。
  • $W^K$为向量$\vec{k}$的转换矩阵，$W^K \in \mathbb{R}^{d \times d_k}$，$d$为词向量的维度，$d_k$为向量$\vec{k}$的维度。
  • $W^V$为向量$\vec{v}$的转换矩阵，$W^V \in \mathbb{R}^{d \times d_v}$，$d$为词向量的维度，$d_v$为向量$\vec{v}$的维度。

由此，我们有 $$ \begin{align} Q &= X \times W^Q \\ K &= X \times W^K \\ V &= X \times W^V \end{align} $$

self_attention_matrix_calculation

最终公式为

$$ \mathsf{Attention}(Q,K,V) = \mathsf{softmax}(\frac{QK^\mathsf{T}}{\sqrt{d_k}})V = Z $$

其中，

$$ \mathsf{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^ne^{z_j}} $$

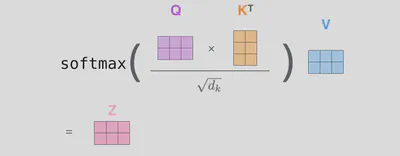
self_attention_matrix_calculation_2

4.3. 多头注意力机制

原始论文中一共使用了8组平行的自注意力层，构成了multi-head机制。

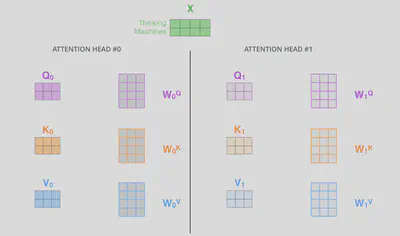
transformer_attention_heads_qkv

前馈神经网络无法同时接受8组平行的自注意力层的输出，所以需要将这8组输出通过某种方式合并为一个矩阵。

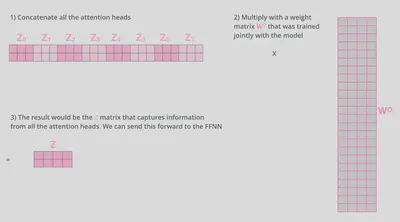
transformer_attention_heads_weight_matrix_o

总全局看，其结构如下所示

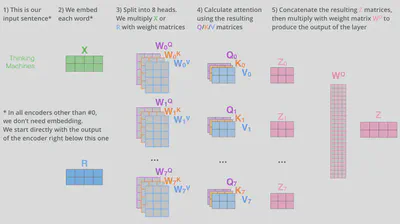
transformer_multi_headed_self_attention_recap

即 $$ \begin{align} \mathsf{MultiHead}(Q, K, V ) &= \mathsf{Concat}(\mathsf{head_1}, ..., \mathsf{head_h})W^O \\ \mathsf{head_i} &= \mathsf{Attention}(XW^Q_i , XW^K_i ,XW^V_i) \end{align} $$

其中 $W^O \in \mathbb{R}^{(h \cdot d_v) \times d}$ ，$h$为平行的自注意力层的层数，$d_v$为向量$\vec{v}$的维度，$d$为词向量的维度。

4.4. 残差连接

在编码器结构中，每个子层之间都有残差连接及layer Normalization连接层。

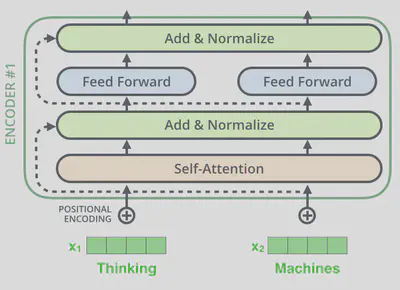
transformer_resideual_layer_norm

放大残差连接及layer Normalization连接层

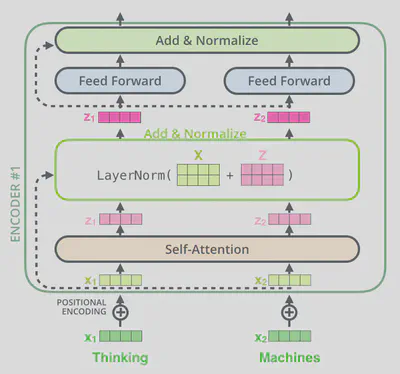
transformer_resideual_layer_norm_2

在解码器中也是如此

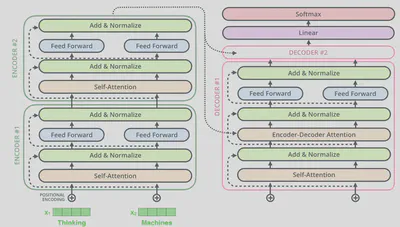
transformer_resideual_layer_norm_3

4.5. Layer Normalization层

层归一化技术可以有效地缓解优化过程中潜在的不稳定、收敛速度慢等问题。

$$ LN(x_i) = \alpha \cdot \frac{x_i - \mu}{\sigma} + b $$

其中 $\mu = \frac{1}{n}\sum^n_{j=1}x_j$ 和 $\sigma = \sqrt{\frac{1}{n}\sum^n_{j=1}(x_j-\mu)^2}$ 分别表示均值和方差，用于将数据平移缩放到均值为 0，方差为 1 的标准分布，$\alpha$和$b$是可学习的参数。

4.6. 前馈层

馈层接受自注意力子层的输出作为输入，并通过一个带有 Relu 激活函数的两层全连接网络对输入进行更加复杂的非线性变换。

$$ FFN(x) = \mathsf{max}(0,xW_1 + b_1)W_2 +b_2 $$

其中 $W1, b1, W2, b2$ 表示前馈子层的参数。实验结果表明，增大前馈子层隐状态的维度有利于提升最终翻译结果的质量，因此，前馈子层隐状态的维度一般比自注意力子层要大。在原论文中，隐藏层的节点数设置为2048。

5. 解码器

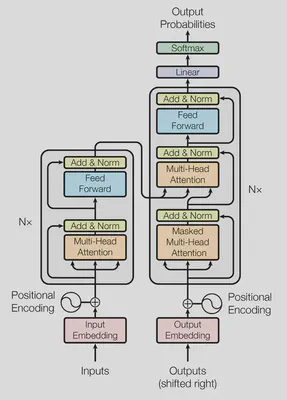
Decoder

从上述结构图可以看出：

  1. 无论编码器或者解码器，数据在输入模型前都必须先加上位置编码。
  2. 编码器的输出将被解码器接受作为输入。
  3. 解码器的第一个自注意力层为"Masked Multi-Head Attention"（掩码多头自注意力层）。这意味着在这一层中模型只关注早于当前输出位置的词，之后位置的编码将被遮挡（通过却其设置为$-\infty$实现）。
  4. 在随后的"Multi-Head Attention"层中，它从解码器的前一层的输出中计算$Q$（query）矩阵，但是其$K$（key）及$V$（value）矩阵由编码器的最终输出提供。

6. 最终输出

模型的最终输出由一个全连接层与softmax层计算得来。

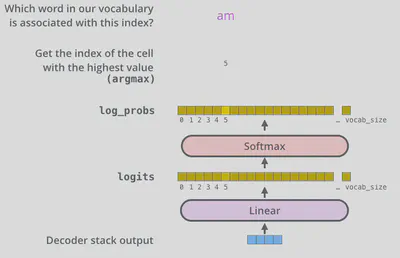
transformer_decoder_output_softmax

全连接层将解码器的最终输出映射到一个logits向量上，其长度等于训练集中所有词语的数量，向量中的每个元素值都对应于该位置所对应的词语的可能性评分。

softmax层则将这些可能性评分转化为概率值，最高值所对应的词语就是最终的输出。

Math Machine Learning
Junhong Liu
Authors
Junhong Liu
Research Assistant