Simulation of Human Reaching with a Robot Arm
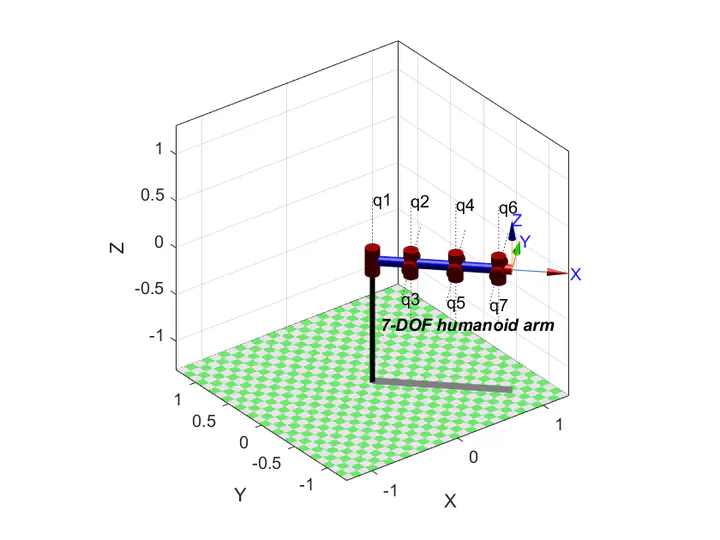
以下为 “Simulation of Human Reaching with a Robot Arm” 项目的概述,该项目用于模拟人类在触摸实验中的手臂运动轨迹。
1. 项目背景
假设场景中存在两个潜在的目标物体 $P_1=(x_1,y_1)$ 与 $P_2=(x_2,y_2)$,$P_1$ 与 $P_2$ 在某一时刻会被同时点亮,此时需要被实验者用手快速触摸亮起红灯的物体,而忽略亮起绿色的物体(在此处,$P_1$ 为红色目标物体,而 $P_2$ 则为绿色干扰物体)。由于人类受到注意力转移机制以及选择历史的影响,人类手臂的运动轨迹并不是笔直指向目标的,所以为了使用机械臂模拟这种现象,我们提出了使用 Sigmoid 函数来规划机械臂的运动轨迹。
2. 算法阐述
要对机械臂进行轨迹规划,我们就需要求解机械臂运动路径中的锚点(waypoint)数据,锚点包括了机械臂末端在该点的位置、速度及加速度信息,这里我们使用五次插值多项式来计算路径的锚点数据。
五次插值多项式一共有 6 个待定参数,所以我们就需要 6 个约束条件才能进行求解。这里假设机械臂运动的启动速度、结束速度、启动加速度与结束加速度都为 0,机械臂的运动时间总步长 $T$ 为超参数,接下来唯一需要求解的约束条件就是机械臂运动路径的总长度 $D$。
2.1. 如何求得机械臂运动路径的总长度 $D$
我们假设机械臂在时间 $t$ 时的运动目标位置为 $P_f(t)$,对于场景中只存在两个物体的情况,$P_f(t)$ 有如下公式:
$$ \begin{aligned} \vec{P}_f(t) &= (\vec{P}_2 - \vec{P}_1)(1 - S(t)) + \vec{P}_1 \\ &= \vec{P}_2(1 - S(t)) + \vec{P}_1 S(t) \end{aligned} $$$$ S(t) = \frac{1}{1 + e^{-t/n}} $$其中 $S(t)$ 为 Sigmoid 函数;$n$ 为时间的缩放因子,用于控制机械臂运动轨迹的弯曲程度,$n$ 越大轨迹越弯曲。从上述式子我们可以看出,$t=0$ 时 $P_f(t)$ 位于 $P_1$ 及 $P_2$ 的几何中心;随着时间的推移 $P_f(t)$ 会快速趋近于目标物体的位置 $P_1$,由此我们便可以模拟出一条指向 $P_1$ 的曲线运动轨迹。
我们假设机械臂的初始位置 $P_0 = (x_0,y_0)$(即锚点 $W^0$ 所在的位置) 是已知的,由此通过计算 $P_f(t)$ 与 $P_0$ 两个位置坐标之间的距离,我们便可以求得机械臂在每个时间步下的运动路径总长度 $D$。
注意:由于 $P_f(t)$ 的位置是变化的,所以路径总长度 $D$ 也是变化的,我们约定使用 $D^t$ 来表示在时间步 $t$ 时 $P_f(t)$ 与 $P_0$ 两个位置坐标之间的距离。
2.2. 通过五次插值多项式计算锚点数据
知道了机械臂运动路径在时间步 $t$ 时的总长度 $D^t$ 以及机械臂的总运动时间步长 $T$,便可以通过五次插值多项式计算机械臂在每个时间步下的锚点数据。此处我们设机械臂在第 $t$ 时间步的运动锚点为 $W^t = [q(t), v(t), a(t)]$,其中 $q(t)$ 为锚点的位置;$v(t)$ 为机械臂在锚点的速度;$a(t)$ 为机械臂在锚点的加速度,通过五次插值多项式可推导得
$$ q(t) = 10(D^t/T^3)t^3 - 15(D^t/T^4)t^4 + 6(D^t/T^5)t^5 \\ v(t) = \dot{q}(t) \\ a(t) = \ddot{q}(t) $$注意:这里我们使用了微分的思想,每个时间步长都设置得非常小,从而利用多条直线轨迹拼接来近似拟合出一条曲线。
2.3. 计算机械臂关节角度
在计算出机械臂的运动轨迹及锚点后,我们就需要利用机器人领域的正、逆运动学算法来计算机械臂每个时刻各个关节的角度,从而使得机械臂的末端可以沿着预定的轨迹进行运行。