Contents

• 1. Introduction
  • 1.1. Large Language Model
  • 1.2. Mixture of Experts
• 2. Theoretical Framework
  • 2.1. The Modern Mixture of Experts
    • 2.1.1. Sparsely-Gated Mixture-of-Experts Layer
    • 2.1.2. Large Language Model Based Mixture of Experts
• 3. Comparative Analysis
  • 3.1. GShard 将 MoE 融入 LLM（2020）
    • 3.1.1. 新的路由机制 / New routing mechanism
  • 3.2. Switch Transformers 简化路由机制，扩大模型规模（2021年）
  • 3.3. WideNet采用共享参数机制，缩小了模型规模（2021年）
  • 3.4. GLaM 与 GShard 模型较为相似（2021年）
  • 3.5. DEMIX 提出模块化构建专家层的思想（2021年）
  • 3.6. PANGU-Σ 提出随机路由专家 (RRE)方法，改进了路由机制（2023）
  • 3.7. 作者通过实验观察发现指令微调对MoE模型有更积极的影响（2023）
• 4. Limitations
• 5. 参考文献 / References
• 6. 附录
  • 6.1. Top-k 路由机制 【5】
  • 6.2. 不同的路由方式 【9】

1. Introduction

1.1. Large Language Model

此处讨论的都是基于 LLM 的 MoE 和 MA 模型，因此我们首先介绍在 LLM 中被广泛使用的 Transformer 架构【7】，以及 LLM 在人工智能和机器学习领域的重要性和相关性。

Transformer 是一种 Sequence to Sequence 架构【13，14】，即模型中包含了编码器与解码器（Encoder-Decoder）。2014 年基于 RNN 的 Sequence to Sequence 架构【13】和基于 Long Short-Term Memory (LSTM) 的 Sequence to Sequence 架构【14】被相继提出，随后在 2017 年 Transformer 被提出用以改进 Sequence to Sequence 架构。对比于 RNN/LSTM 架构，Transformer 具有以下几个方面具有显著优势：

• 并行运算：与只能顺序处理数据的 RNN/LSTM 架构不同，Transformer 可以并行处理多个序列数据，从而显著缩短训练时间。这一特性使得 Transformer 具有高度可扩展性，能够高效地处理大量数据和长序列，直接推动了 LLM 的发展。

• 处理长程依赖关系：Transformer 模型通过位置编码及自注意力机制等方式，使其可以直接对序列中任意两个位置之间的关系进行建模，权衡输入数据不同部分之间的影响，从而处理输入数据之间的长程依赖关系。而 RNN 由于梯度消失或爆炸等问题，尽管 LSTM 的设计在一定程度上缓解这个问题，但这些模型在处理长程依赖问题上还是弱于 Transformer。这使得 Transformer 架构可以帮助模型处理长上下文的数据，进一步推动了 LLM 的发展。

（To the best of our knowledge）基于我们现有的知识，，最早的 LLM 是基于 Transformer 的 GPT【29】。如今，基于 Transformer 架构的 LLM 已经在各个领域取得了惊人的表现。。。（综述中补充）

1.2. Mixture of Experts

Mixture of Experts（MoEs） 概念从提出到现在已有 30 多年，其在机器学习中的应用可以追溯到 1994 提出的用于监督学习的树状架构 Hierarchical Mixture-of-Experts（HMEs）【1】，使用 Expectation-Maximization（EM）算法【3】来训练并更新模型。下图展示了一个双层 HMEs（two-level hierarchical mixture-of-experts）结构。

$x$ 是输入向量；

$e_{ij}$ 表示第二层第 $i$ 个节点的第 $j$ 个专家的输出，所有专家都是一个“广义线性（generalized linear）网络”【2】，有如下定义：

其中 $U_{ij}$ 是权重矩阵，$f$ 是一个固定的，连续的，非线性的函数（$f$ is a fixed continuous nonlinearity）；

$g_{ij}$ 与 $g_i$ 皆为路由网络的输出，有如下定义：

同理

其中 $v_i$ 与 $v_{ij}$ 皆为权重向量；

$\mu_i$ 表示第二层第 $i$ 个节点的输出，$\mu$ 为第一层的输出，有如下定义：

HMEs 是一种分治算法（divide-and-conquer algorithms），其将复杂的输入空间显式地分为多个更简单的子空间，从而使模型能更快地拟合数据，加速训练过程。HMEs 最大的优点是使用了统计的方法，构建了统一的框架来处理任何类型的输入与输出数据。

（These algorithms fit surfaces to data by explicitly dividing the input space into a nested sequence of regions, and by fitting simple surfaces (e.g., constant functions) within these regions. The advantages of these algorithms include the interpretability of their solutions and the speed of the traiining process.） （The major advantage of the HME approach over related decision tree and multivariate spline algorithms such as CART, MARS and ID3 is the use of a statistical framework. The statistical framework motivates some of the variance-decreasing features of the HME approach, such as the use of “soft” bsundaries. The statistical approach also provides a unified framework for handling a variety of data types, including binary variables, ordered and unordered categorical variables, and real variables, both at the input and the output.）

近年来大模型（LLMs）在各个领域都取得了让人惊叹的表现，有研究表明更大规模的训练是提高语言模型性能的一个有效途径【4】，但受限于计算效率与开销等问题，一味地扩大模型规模并不现实。于是【5】等人在 GNMT 模型（一种 LSEM 模型）【6】的基础上提出了稀疏专家模型（Sparse MoE），该模型减小了 LSTM 层的数量并嵌入了 MoE 层，以较低的计算开销在大型语言建模及机器翻译基准测试中（large language modeling and machine translation benchmarks）取得了当时最先进的结果。GNMT 模型是一种 Recurrent Neural Network（RNN）神经网络，而 Transformer 架构【7】的出现改进了 RNN 网络的计算效率，奠定了当代大模型的基础，因此【5】等人的研究影响了现今大多数基于 LLM 的 MoE 模型的研究设计。

现代基于LLM 的 MoE 模型通过一个门控网络（Gating Network）将输入空间（input space）划分为多个子空间，再由多个专家网络（Expert Network，以下简称专家）分别处理特定的子空间，最终得到整体的预测结果,混合专家模型每个专家都是针对不同的数据子空间进行训练 【8】。随着大模型的规模不断扩大，模型的训练与预测都会产生很大的计算成本，MoE 通过这种方式可以将模型计算量与模型规模分离开来，从而得到一个庞大但高效的大模型【9，10】。

MoE 与 LLM 的结合赋予了模型新的特性：

• 效率和可扩展性：MoE 架构中门控网络可将输入路由给不同的专家，这使得不同的专家可以针对特定领域的任务进行训练及预测。同时这种动态分配计算资源的方式能更有效地扩展模型，减少模型的计算需求，更有效地利用资源并扩展模型。

• 专业化和性能：通过将模型划分为专门从事不同领域的专家，模型可以在特定任务上获得比通用模型更高的性能，提高预测准确性。此外不同专家之间也可以相互合作，以处理更广泛、更复杂的任务 。

• 灵活性和适应性：通过添加针对特定任务或领域的新专家，可以更轻松地调整或扩展 MoE 系统，而无需重新训练整个模型。 这使得模型更容易跟上新兴趋势或扩展其功能。

• 终身学习能力：MoE 结构的特性使得模型可以在面对新的数据分布时引入新的专家进行学习，从而扩展模型能力而不过分增加计算成本，而模型之前学习到的知识仍然将会保留【11，12】

2. Theoretical Framework

2.1. The Modern Mixture of Experts

2.1.1. Sparsely-Gated Mixture-of-Experts Layer

（To the best of our knowledge）基于我们现有的知识，最早设计出 MoE 嵌入层并将其运用到 Sequence to Sequence 架构的是【5】等人。如下图所示，他们将一个 MoE 层嵌入到了相邻的两个 LSTM 堆叠层（stacked LSTM layers）之间，层与层之间都使用残差连接（residual connections）【16】。【5】等人在编码器中嵌入了 3 个 LSTM 层，MoE 层位于第 2 与第 3 个 LSTM 层之间；在解码器中嵌入了 2 个 LSTM 层，MoE 层位于第 1 与第 2 个 LSTM 层之间。

MoE 层结构以上图所示为例，输入 $X$ 被路由网络路由到 TOP-2 的两个专家 Expert 2 与 Expert i 中，然后专家网络的输出经过加权再相加后便是 MoE 层的最终输出。数学表达式如下：

为了减小计算量，【5】等人提出了带噪声的 TOP-K 的路由机制（Noisy Top-K Gating），该机制1. 通过 TOP-K 的路由机制减小了计算量 2. 通过引入噪声来达到负载均衡，使得所有专家都能得到充分训练。实现方法如下：

高斯噪声（即$\mathsf{StandNormal}()$）的大小由 $\mathsf{Softplus}((X \cdot W_{noise})_i)$ 控制，$W_{noise}$ 是一个权重矩阵。$\mathsf{Softplus}(x)$ 函数的形式如下所示：

其中专家为前馈网络（feed forward network），路由网络与专家同时训练，采用反向传播法（back-propagation）更新参数。

2.1.2. Large Language Model Based Mixture of Experts

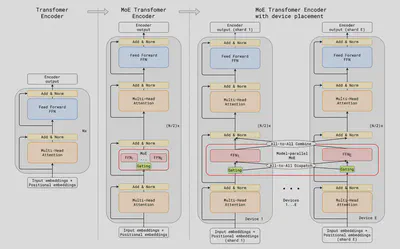
【17】等人参考【5】等人的研究，提出了首个基于 Transformer 架构的 Large Language Model Based Mixture of Experts（以下简称 LLM-MoE）模型，GShard。其 MoE 层结构如下图所示，左边传统的稠密 Transformer 架构的 LLM 对于每一个输入，都需要在完整的模型中进行计算。而右边基于 MoE 的稀疏 Transformer 架构的 LLM 对于每一个输入，只有少部分专家（参数）被激活，大部分专家（参数）处于未激活状态。在这里，GShard 模型将专家替换为了前馈网络 (FFN)

稠密模型（左）将两个输入 (token) 发送到相同的前馈网络 (FFN)，使用相同的参数。稀疏模型（右）将两个输入经由路由网络在四个专家之间 (FFN1, …, FFN4) 独立路由。虽然每个模型的计算量无太大差别，但稀疏模型具有更多的总参数量。

3. Comparative Analysis

3.1. GShard 将 MoE 融入 LLM（2020）

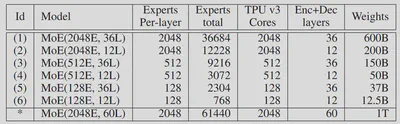
论文名称：GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding 【17】 论文作者：D. Lepikhin et al. 提出时间：2020年 所属机构：Google 提出模型：GShard 基座模型：Transformer模型 参数规模：最大为 1000 B 论文简介： GShard 参考 Shazeer 等人 (2017) 【5】 的做法，将 Transformer 的编码器 (encoder) 和解码器 (decoder) 中的前馈神经层（FFN）替换成 MoE 层。当允许模型进行分布式部署时，每个专家都被独立部署在一台设备上并被所有设备共享，但模型的其他参数是相同的。此外，GShard 改进了路由机制。

3.1.1. 新的路由机制 / New routing mechanism

• 固定专家的容量。每个专家处理的 token 数量不得超过一定阈值，否则就将超出容量的 token 抛弃。假设一个 batch 里包含的 token 数量为 $N$，专家总数为 $E$。则阈值可以被设置为趋近于 $(N / E)$ 的一个整数。
• 本地调度分组 (Local group dispatching)。将一个 batch 里包含的所有 token 分为 $G$ 组，每组包含 $S = N / G$ 个 token。然后给每个组分配专家容量，即每个专家在每个组最多接收 $2N / (G \times E)$ 个token （注意这里使用的是 top-2 路由规则，所以上式在计算式乘与了 2）
• 设置辅助损失 (Auxiliary loss) 参数。将辅助损失 (Auxiliary loss) 参数融入到整体损失函数中，进而约束模型尽量将 token 均匀路由到每个专家。
• 随机路由 (Random routing)。通常来说，采用 top-2 路由规则将使每个 token 被路由到得分最大的两个专家。但如果第二个专家分数较低的话，则可以考虑忽略。所以对于第二个专家，将根据其路由得分的情况，以相应概率选择是否路由。

3.2. Switch Transformers 简化路由机制，扩大模型规模（2021年）

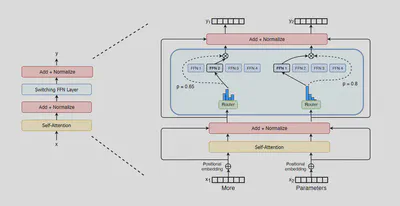
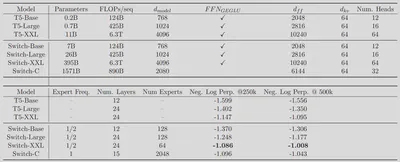
论文名称：Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity 【18】 论文作者：W. Fedus, B. Zoph, and N. Shazeer 提出时间：2021年 所属机构：Google 提出模型：Switch Transformers 基座模型：Transformer模型 参数规模：1571 B 论文简介： Switch Transformers 致力于以一种简单高效的方式，尽可能地把Transformer模型的参数量做大。并认为进行大规模训练是通向强大模型的有效途径，具有大量数据集和参数量的简单体系结构可以超越一些复杂的算法。 所以相比于Shazeer等人【5】提出的 top-k (k>1) 路由机制，Switch Transformers简化了 MoE 的路由算法，采用 top-1 路由机制，从而提高了计算效率。

3.3. WideNet采用共享参数机制，缩小了模型规模（2021年）

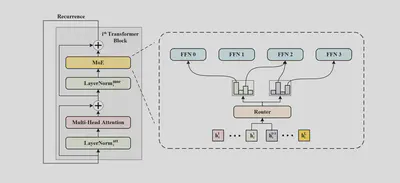
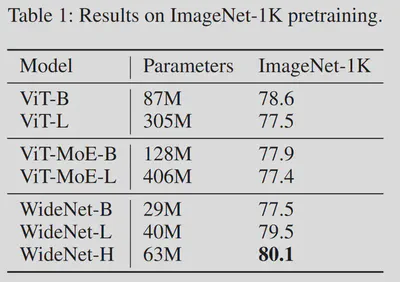
论文名称：Go Wider Instead of Deeper 【19】 论文作者：F. Xue et al. 提出时间：2021年 所属机构：National University of Singapore 提出模型：WideNet 基座模型：Transformer模型 参数规模：最大为 63 M 论文简介： 在论文中，作者提出了一种新框架WideNet，尝试解决如何在压缩模型参数量的情况下取得更好效果的问题。该框架最核心的创新在于采用了共享参数（recurrence）机制：即共享MoE层及Multi-Head Self-Attention层的参数。但为了保证语义的多样性，Norm层的参数并不会被共享。

3.4. GLaM 与 GShard 模型较为相似（2021年）

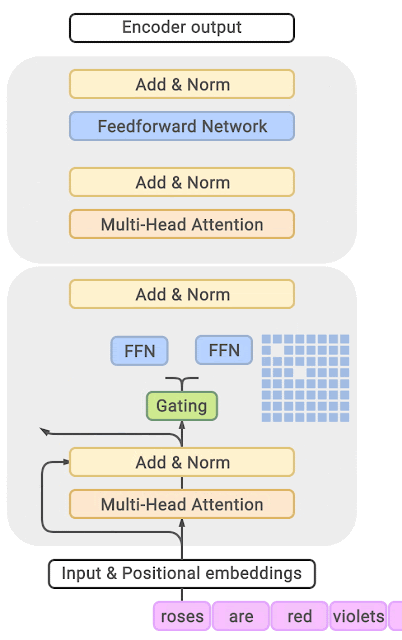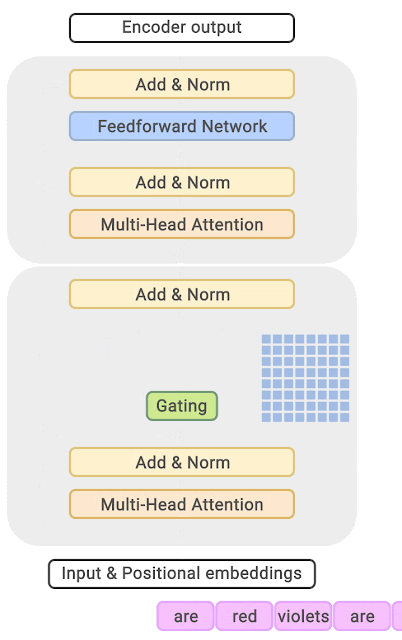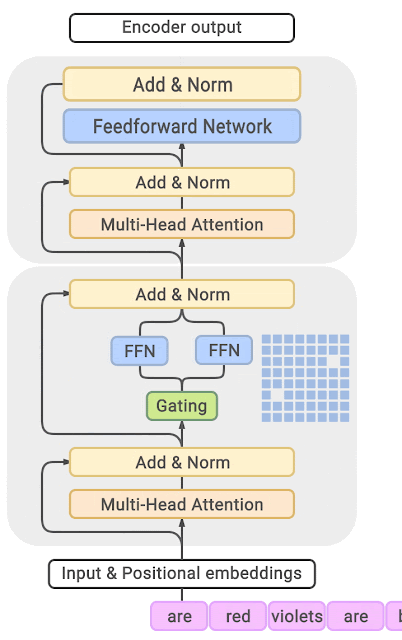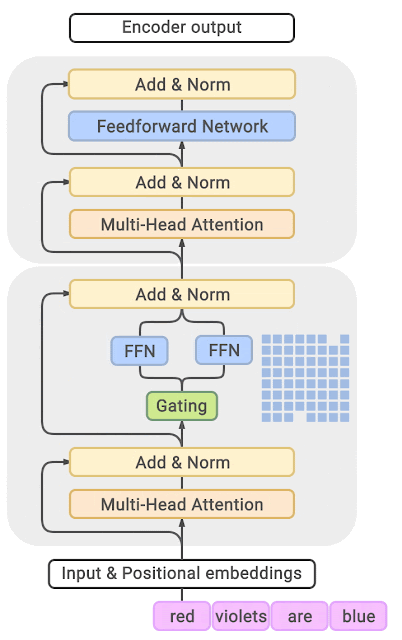
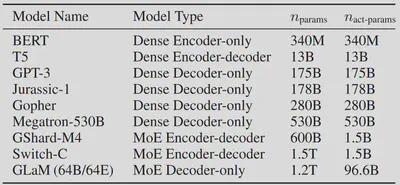
论文名称：GLaM: Efficient Scaling of Language Models with Mixture-of-Experts 【20】 论文作者：N. Du et al. 提出时间：2021年 所属机构：Google 提出模型：GLaM 基座模型：Transformer模型 参数规模：未激活：1200 B / 激活后：96.6 B 论文简介： GLaM由Google在2021年提出，共有1.2万亿个参数，但模型运行时只有大约966亿参数被激活。GLaM的做法是在Transformer层之间添加一个MoE层，对于每个token，门控模型会动态地从64个候选专家中选择2个最相关的专家进行预测，并将这2个专家地输出通过加权的方式传递给下一个Transformer层。 同时，该论文比较了数据数量与数据质量对模型的影响，发现不能一味追求数据的规模，数据的质量对模型影响更大。

3.5. DEMIX 提出模块化构建专家层的思想（2021年）

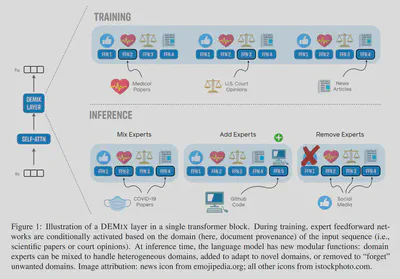
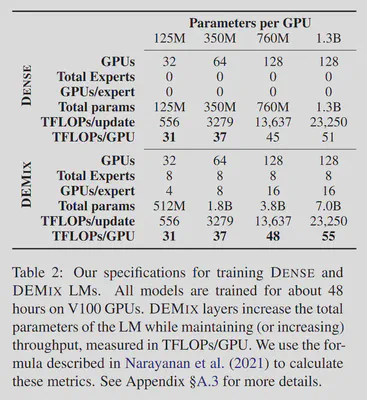
论文名称：DEMIX Layers: Disentangling Domains for Modular Language Modeling 【21】 论文作者：S. Gururangan et al. 提出时间：2021年 所属机构：Allen Institute for AI，Facebook AI Research 提出模型：DEMIX 基座模型：Transformer模型 参数规模：1.3 B 论文简介： 在训练期间，模型会根据输入 tokrn（即科学论文或法庭意见）的相关任务或领域有条件地激活相应专家。因此每个样本需要做相关领域的标记，每个专家负责一个领域，采用显式路由。

在推理时，输入的 token 不需要有领域标记，由模型隐式地路由到不同专家。同时，语言模型可以混合已有的领域专家来处理异构领域或新领域任务，或添加领域专家以适应新领域，或删除领域专家以“忘记”不需要的领域。

3.6. PANGU-Σ 提出随机路由专家 (RRE)方法，改进了路由机制（2023）

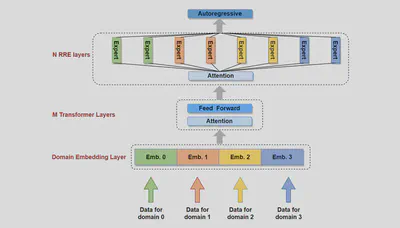
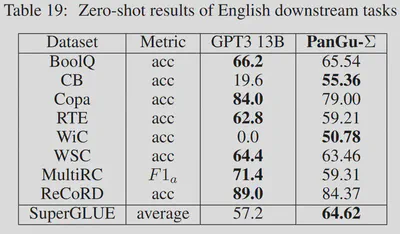
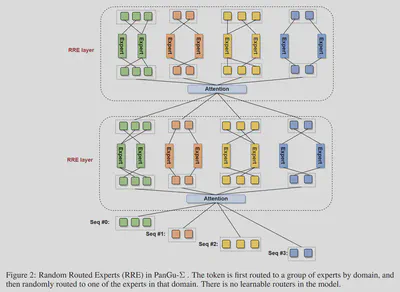
论文名称：PANGU-Σ: TOWARDS TRILLION PARAMETER LANGUAGE MODEL WITH SPARSE HETEROGENEOUS COMPUTING 【22】 论文作者：X. Ren et al. 提出时间：2023年 所属机构：HuaWei 提出模型：PANGU-Σ 基座模型：PanGu-α模型【23】 参数规模：1085 B 论文简介： PANGU-Σ 参考 Roller 等人 (2021) 【24】 提出的 Hash Layers 思想，提出了随机路由专家（RRE）方法，论文宣称其英文下游任务可以与GPT-13B相媲美。

RRE做了双层的设计： 第一层： 根据相关领域或任务，将 token 分配给不同的专家组（多个expert构成一个专家组，供一个 task / domain 使用）。 第二层： 参照 Hash Layers 思想，静态路由 token 到专家组内的专家，从而让所有专家可以负载均衡。该层没有可学习的参数，故速度更快。

3.7. 作者通过实验观察发现指令微调对MoE模型有更积极的影响（2023）

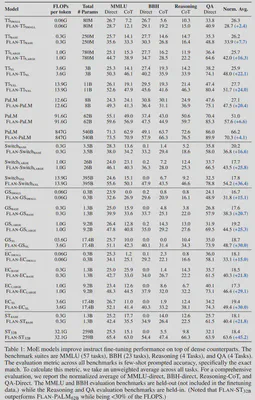
论文名称：Mixture-of-Experts Meets Instruction Tuning:A Winning Combination for Large Language Models 【25】 论文作者：S. Shen et al. 提出时间：2023年 所属机构：Google 提出模型：FLAN 基座模型：不适用 参数规模：不适用 论文简介：该论文强调了指令微调对MoE模型的影响，认为将指令微调运用在MoE模型上将有助于提高模型性能。

4. Limitations

1. 训练和推理的复杂性：LLM-MoE 模型本质上比传统的密集模型更复杂。 将输入路由到不同专家的门控机制增加了额外的复杂性，使得训练和推理过程难以优化。

2. 负载平衡：由于门控机制的存在，模型中一些专家可能被过度训练，而另一些专家则未被充分利用，从而导致模型性能下降。 实现最佳负载平衡需要复杂的算法，并且可能对模型的超参数和数据的性质敏感。

3. 增加模型大小：LLM-MoE 相对而言通常具有更大的参数总量，这会导致训练和部署的内存需求增加，从而提高模型对硬件的要求。

4. 并行化困难：将输入动态路由到不同的专家可能会对 GPU 或 TPU 之间的通信能力造成挑战，限制硬件的并行计算能力。且工作负载可能是不规则且不可预测的，从而使跨硬件资源的计算分配变得复杂。

5. 可解释性和调试：LLM-MoE 模型的复杂性增加可能会使它们更难以解释和调试。 与更简单、密集的模型相比，理解为什么选择特定专家来处理给定的输入或诊断模型行为中的问题可能更具挑战性。

5. 参考文献 / References

1. M. I. Jordan, “Hierarchical mixtures of experts and the EM algorithm,” Neural Comput., vol. 6, no. 2, pp. 181–214, 1994.
2. McCullagh, P. & Nelder, J.A. (1983). Generalzzed Lznear Models. London: Chapman and Hall.
3. Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statzstzcal Soczety, B, 39, 1-38.
4. Jared Kaplan, Sam McCandlish, Tom Henighan, Tom B Brown, Benjamin Chess, Rewon Child, Scott Gray, Alec Radford, Jeffrey Wu, and Dario Amodei. Scaling laws for neural language models. arXiv preprint arXiv:2001.08361, 2020.
5. Noam Shazeer, Azalia Mirhoseini, Krzysztof Maziarz, Andy Davis, Quoc Le, Geoffrey Hinton, and Jeff Dean. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. arXiv preprint arXiv:1701.06538, 2017.
6. Yonghui Wu, Mike Schuster, Zhifeng Chen, Quoc V. Le, Mohammad Norouzi, Wolfgang Macherey, Maxim Krikun, Yuan Cao, Qin Gao, Klaus Macherey, Jeff Klingner, Apurva Shah, Melvin Johnson, Xiaobing Liu, Łukasz Kaiser, Stephan Gouws, Yoshikiyo Kato, Taku Kudo, Hideto Kazawa, Keith Stevens, George Kurian, Nishant Patil, Wei Wang, Cliff Young, Jason Smith, Jason Riesa, Alex Rudnick, Oriol Vinyals, Greg Corrado, Macduff Hughes, and Jeffrey Dean. Google’s neural machine translation system: Bridging the gap between human and machine translation. arXiv preprint arXiv:1609.08144, 2016.
7. A. Vaswani et al., “Attention Is All You Need.” arXiv, Aug. 01, 2023. Accessed: Sep. 15, 2023. [Online]. Available: http://arxiv.org/abs/1706.03762
8. T. Baldacchino, E. J. Cross, K. Worden, and J. Rowson, “Variational Bayesian mixture of experts models and sensitivity analysis for nonlinear dynamical systems,” Mechanical Systems and Signal Processing, vol. 66–67, pp. 178–200, Jan. 2016, doi: 10.1016/j.ymssp.2015.05.009.
9. W. Fedus, J. Dean, and B. Zoph, “A Review of Sparse Expert Models in Deep Learning,” arXiv.org. Accessed: Dec. 05, 2023. [Online]. Available: https://arxiv.org/abs/2209.01667v1
10. David Patterson, Joseph Gonzalez, Quoc Le, Chen Liang, Lluis-Miquel Munguia, Daniel Rothchild, David So, Maud Texier, and Jeff Dean. Carbon emissions and large neural network training. arXiv preprint arXiv:2104.10350, 2021.
11. Lifelong Language Pretraining with Distribution-Specialized Experts
12. MoRAL: MoE Augmented LoRA for LLMs’ Lifelong Learning
13. Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation
14. Sutskever, Ilya, Vinyals, Oriol, and Le, Quoc V. Sequence to Sequence Learning with Neural Networks. In Proc. of NIPS, pp. 3104–3112, 2014.
15. Convolutional Sequence to Sequence Learning
16. Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. IEEE Conference on Computer Vision and Pattern Recognition, 2015.
17. D. Lepikhin et al., “GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding.” arXiv, Jun. 30, 2020. doi: 10.48550/arXiv.2006.16668.
18. W. Fedus, B. Zoph, and N. Shazeer, “Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity,” arXiv.org. Accessed: Nov. 29, 2023. [Online]. Available: https://arxiv.org/abs/2101.03961v3
19. F. Xue, Z. Shi, F. Wei, Y. Lou, Y. Liu, and Y. You, “Go Wider Instead of Deeper,” arXiv.org. Accessed: Nov. 29, 2023. [Online]. Available: https://arxiv.org/abs/2107.11817v3
20. N. Du et al., “GLaM: Efficient Scaling of Language Models with Mixture-of-Experts,” arXiv.org. Accessed: Nov. 29, 2023. [Online]. Available: https://arxiv.org/abs/2112.06905v2
21. S. Gururangan, M. Lewis, A. Holtzman, N. A. Smith, and L. Zettlemoyer, “DEMix Layers: Disentangling Domains for Modular Language Modeling,” arXiv.org. Accessed: Dec. 05, 2023. [Online]. Available: https://arxiv.org/abs/2108.05036v2
22. X. Ren et al., “PanGu-Σ: Towards Trillion Parameter Language Model with Sparse Heterogeneous Computing.” arXiv, Mar. 19, 2023. doi: 10.48550/arXiv.2303.10845.
23. Wei Zeng, Xiaozhe Ren, Teng Su, Hui Wang, Yi Liao, Zhiwei Wang, Xin Jiang, ZhenZhang Yang, Kaisheng Wang, Xiaoda Zhang, Chen Li, Ziyan Gong, Yifan Yao, Xinjing Huang, Jun Wang, Jia xin Yu, Qiwei Guo, Yue Yu, Yan Zhang, Jin Wang, Heng Tao, Dasen Yan, Zexuan Yi, Fang Peng, Fan Jiang, Han Zhang, Lingfeng Deng, Yehong Zhang, Zhengping Lin, Chao Zhang, Shaojie Zhang, Mingyue Guo, Shanzhi Gu, Gaojun Fan, Yaowei Wang, Xuefeng Jin, Qun Liu, and Yonghong Tian. Pangu-α: Large-scale autoregressive pretrained chinese language models with auto-parallel computation. ArXiv, abs/2104.12369, 2021.
24. S. Roller, S. Sukhbaatar, A. Szlam, and J. Weston, “Hash Layers For Large Sparse Models.” arXiv, Jul. 20, 2021. doi: 10.48550/arXiv.2106.04426.
25. S. Shen et al., “Mixture-of-Experts Meets Instruction Tuning:A Winning Combination for Large Language Models.” arXiv, Jul. 05, 2023. doi: 10.48550/arXiv.2305.14705.
26. Y. Zhou et al., “Mixture-of-Experts with Expert Choice Routing,” arXiv.org. Accessed: Nov. 29, 2023. [Online]. Available: https://arxiv.org/abs/2202.09368v2
27. M. Lewis, S. Bhosale, T. Dettmers, N. Goyal, and L. Zettlemoyer, “BASE Layers: Simplifying Training of Large, Sparse Models.” arXiv, Mar. 30, 2021. doi: 10.48550/arXiv.2103.16716.
28. Bertsekas, Dimitri P. “Auction algorithms for network flow problems: A tutorial introduction.” Computational optimization and applications 1 (1992): 7-66.
29. Radford, A., Narasimhan, K., Salimans, T., & Sutskever, I. (2018). Improving language understanding by generative pre-training. OpenAI. https://s3-us-west-2.amazonaws.com/openai-assets/research-covers/language-unsupervised/language_understanding_paper.pdf

6. 附录

6.1. Top-k 路由机制 【5】

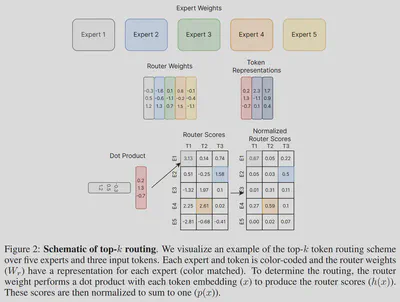
以上图为例，我们假设MoE层中存在： 5个专家：Expert 1, Expert 2, Expert 3, Expert 4, Expert 5 3个token输入：T1, T2, T3

则有： 路由矩阵 $R$，其大小为 $d \times n_e$ ； Token矩阵 $T$，其大小为 $d \times n_t$ 。 其中，$d$ 表示token的向量长度，$n_e$ 表示专家的数量，$n_t$ 表示token的数量。此处，$d = 3$，$n_e = 5$，$n_t = 3$。

由此可得，路由得分矩阵

$H(T)$ 与 $P(T)$ 的大小为 $n_e \times n_t$ 。

举例：单独计算输入 T1 对于专家 Expert 1 的路由得分 $p_1$

我们有

可得 Expert 1 对应的路由得分 $h(t)_1$ 为

在得到 $h(t)_i$ 后，再经过 $softmax$ 函数运算对结果进行归一化，就是最终的路由得分 $p_1$，

其中，$N$ 表示所有专家的数量。

以上方法只是对于单一输入的例子，对于批量输入，可以利用矩阵的形式提高运算效率

计算可得：

Python代码实现：

import numpy as np

# 设定数据
T = np.array([[0.2 , 2.3 , 1.7],[1.3 , -1.1 , 0.9],[-0.7 , 0.1 , 0.4]])
R = np.array([[-0.3 , -1.6 , 0.1 , 0.8 , -0.1],[0.5 , -0.6 , -1.1 , -0.2 , -0.4],[1.2 , 1.3 , 0.7 , 1.5 , -1.1]])

# 计算路由得分矩阵
H = np.dot(R.T,T)
print(H)

# 计算softmax后的路由得分矩阵
P = np.exp(H) / sum(np.exp(H))
print(P)

# results:
# [[-0.25 -1.12  0.42]
#  [-2.01 -2.89 -2.74]
#  [-1.9   1.51 -0.54]
#  [-1.15  2.21  1.78]
#  [ 0.23  0.1  -0.97]]
# [[0.2952693  0.02156584 0.17951429]
#  [0.05079957 0.00367337 0.00761603]
#  [0.05670644 0.29919948 0.06873474]
#  [0.12004754 0.60251376 0.69942237]
#  [0.47717716 0.07304754 0.04471258]]

对于该MoE层的最终输出 $y$

其中，$p_i(t)$ 为专家 $i$ 所对应的 $softmax$ 后的路由得分，$E_i(t)$ 为专家 $i$ 的输出， $\mathcal{T}$ 表示路由得分 top-k 的专家的集合。

6.2. 不同的路由方式 【9】

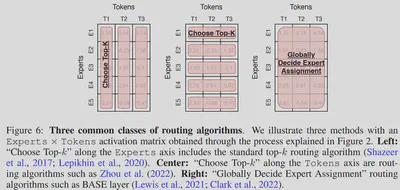
每个 token 选择 top-k 的专家 / Each token chooses the top-k experts

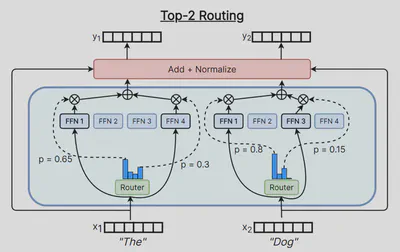
以 top-2 路由机制为例，Shazeer 等人 (2017) 【5】 及 Lepikhin 等人 (2020) [11] 以输入为基准，每个输入都将路由到路由得分最高的两个专家。这样做的一个坏处是每个专家的负载是不均衡的，容易造成计算资源的浪费。

每个专家选择 top-k 的 token / Each expert chooses the top-k tokens

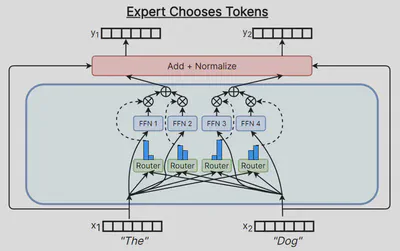
Zhou 等人 (2022) 【26】 以专家为基准，每个专家都会选择路由得分最高的 k 个输入（token）。 现在每个专家将始终拥有相同数量的输入（token），尽管某些输入可能不会路由到任何专家，或者某些输入可能路由到所有专家。 但根据实验观察，该算法表现良好，并且具有自适应计算解释，其中模型可以隐式地将更多计算资源应用于某些输入。

全局决定 token 的路由分配 / Globally determine what tokens should go to each expert

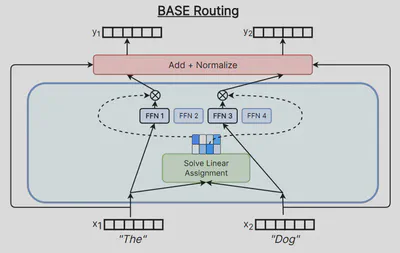
Lewis 等人于2021年提出 BASE 层架构 【27】，其将路由分配问题转化为线性分配问题。

假设已知路由得分矩阵 $H$，约定： $H_{ij}$ 表示得分矩阵 $H$ 的第 $i$ 行第 $j$ 列，即专家 $i$ 对于每个输入 (token) $j$ 所对应的路由得分。

假设存在路由分配矩阵 $A$，约定： $A_{ij}$ 表示分配矩阵 $A$ 的第 $i$ 行第 $j$ 列，即专家 $i$ 对于每个输入 (token) $j$ 的分配状态。 元素值 1 表示将输入 $j$ 分配给专家 $i$，否则元素值为 0。

故存在优化问题，其 目标函数：

优化约束：

其中，$T$ 表示输入 (token) 的数量，$E$ 表示专家的数量。

原论文中，Lewis 等人使用的是 Bertsekas (1992) 【28】 提出的竞拍算法 (auction algorithm) 求解以上问题。