Vision Transformer - LLM Architecture
Implementation : My Github
Note: this implementation is based on this Blog, many thanks to the author for sharing.
Vision Transformer (ViT)
ViT - Blogs for reference: Chinese1、Chinese2、Chinese3、Chinese4
ViT - Codes for reference: Github1
ViT - Reference: 《An Image is Worth 16x16 words Transformers for image recognition at scale》
An overview of the ViT model is depicted in below Figure.
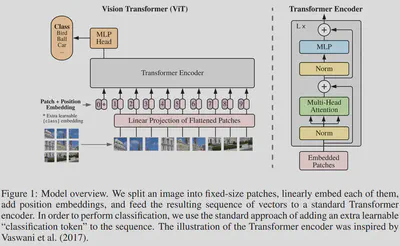
The standard Transformer receives as input a 1D sequence of token embeddings.
Thus, we need to reshape the 2D image $x \in \mathbb{R}^{H \times W \times C}$ into a sequence of flattened 2D patches $x_p \in \mathbb{R}^{N \times (P^2 \cdot C)}$, where
- $(H, W)$ is the resolution of the original image,
- $C$ is the number of channels,
- $(P, P)$ is the resolution of each image patch,
- $N = H \cdot W / P^2$ is the resulting number of patches, which also serves as the effective input sequence length for the Transformer.
The Transformer uses constant latent vector size $D$ through all of its layers, so we flatten the patches and map to $D$ dimensions with a trainable linear projection. We refer to the output of this projection as the patch embeddings. $$ z_0 = [x_{class}; x_p^1E; x_p^2E; ...; x_p^NE] + E_{pos}, \quad E \in \mathbb{R}^{(P^2 \cdot C) \times D}, E_{pos} \in \mathbb{R}^{(P^2 \cdot C) \times D} $$
Similar to BERT’s [class] token, we prepend a learnable embedding ($z_0^0 = x_{class}$) to the sequence of embedded patches, whose state at the output of the Transformer encoder ($z^0_L$) serves as the image representation $y$. Both during pre-training and fine-tuning, a classification head is attached to $z^0_L$. The classification head is implemented by a MLP with one hidden layer at pre-training time and by a single linear layer at fine-tuning time. $$ \begin{aligned} z'_l &= MSA(LN(z_{l-1})) + z_{l-1}, \quad &l = 1 ... L \\ z_l &= MLP(LN(z'_l)) + z'_l, \quad &l = 1 ... L \\ y &= LN(z^0_L) \end{aligned} $$
Position embeddings are added to the patch embeddings to retain positional information. We use standard learnable 1D position embeddings, since no significant performance gained by using more advanced 2D-aware position embeddings. The resulting sequence of embedding vectors serves as input to the encoder.
Multihead Self-Attention (MSA)
MSA - Blogs for reference: Chinese1
MSA - Reference: 《Attention Is All You Need》
Transformer
Transformer - Blogs for reference: English1、Chinese1、Chinese2
Transformer - Codes for reference: Harvard
Transformer - Reference: 《Attention Is All You Need》
Positional Encoding
PE - Codes for reference: Github1
PE - Reference: 《Attention Is All You Need》
Skip Connection (残差连接)
SC - - Blogs for reference: Chinese1
Self-Attention (SA)
Codes
Reference Blog: Chinese
导入依赖
import torch
from torch import nn, einsum
import torch.nn.functional as F
from einops import rearrange, repeat
from einops.layers.torch import Rearrange
pair函数
def pair(t):
return t if isinstance(t, tuple) else (t, t)
- 该函数用于确保返回的数据类型是元组。如果
t是元组,返回t;否则返回元组(t, t) isinstance(t, tuple)函数用于判断t是否为tuple(元组)类型的数据实例
PreNorm
class PreNorm(nn.Module):
def __init__(self, dim, fn):
super().__init__()
self.norm = nn.LayerNorm(dim)
self.fn = fn
def forward(self, x, **kwargs):
return self.fn(self.norm(x), **kwargs)
PreNorm类继承自父类nn.Module。详情见Pytorch-nn.Module模块详解- **kwargs 是一种灵活传参方式。详情见灵活传递参数
- 此处需重点理解
self.fn(self.norm(x), **kwargs)命令,该命令用于实现以下两个公式: $$ \begin{aligned} z'_l &= MSA(LN(z_{l-1})) + z_{l-1}, \quad &l = 1 ... L \\ z_l &= MLP(LN(z'_l)) + z'_l, \quad &l = 1 ... L \end{aligned} $$
其中,self.norm(x)实现$LN(z_{l-1})$及$LN(z'_l)$操作,并将结果作为输入传入self.fn()所表示的函数;而self.fn()用于实现$MLP()$及$MSA()$操作,即调用下文的FeedForward及Attention函数,其中**kwargs实现灵活传参
- 如果你对
nn.LayerNorm()感到疑惑,参见此博客
MLP
class FeedForward(nn.Module):
def __init__(self, dim, hidden_dim, dropout = 0.):
super().__init__()
self.net = nn.Sequential(
nn.Linear(dim, hidden_dim),
nn.GELU(),
nn.Dropout(dropout),
nn.Linear(hidden_dim, dim),
nn.Dropout(dropout)
)
def forward(self, x):
return self.net(x)
- 该函数实现多层感知机功能,由线性层、激活函数GRLU和Dropout实现
- 参数
dim表示输入和输出的数据维度 - 参数
hidden_dim表示中间层的维度 - 参数
dropout表示随机抛弃数据的概率,详情参见此Blog
MSA
class Attention(nn.Module):
def __init__(self, dim, heads = 8, dim_head = 64, dropout = 0.):
super().__init__()
inner_dim = dim_head * heads
project_out = not (heads == 1 and dim_head == dim)
self.heads = heads
self.scale = dim_head ** -0.5
self.attend = nn.Softmax(dim = 1)
self.to_qkv = nn.Linear(dim, inner_dim * 3, bias = False)
self.to_out = nn.Sequential(
nn.Linear(inner_dim, dim),
nn.Dropout(dropout),
) if project_out else nn.Identity()
def forward(self, x):
b, n, _, h = *x.shape, self.heads
qkv = self.to_qkv(x).chunk(3, dim = -1)
q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h = h), qkv)
dots = einsum('b h i d, b h j d -> b h i j', q, k) * self.scale
attn = self.attend(dots)
out = einsum('b h i j, b h j d -> b h i d', attn, v)
out = rearrange(out, 'b h n d -> b n (h d)')
return self.to_out(out)
- 该函数用于实现Transformer的核心功能Multi-Head Attention
heads表示head的数量dim_heads表示单个head的输出数据的维度- 该函数实现公式: $$ Attention(Q, K, V) = softmax(\frac{QK^\mathsf{T}}{\sqrt{d_k}})V $$
Transformer
class Transformer(nn.Module):
def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout = 0.):
super().__init__()
self.layers = nn.ModuleList([])
for _ in range(depth):
self.layers.append(nn.ModuleList([
PreNorm(dim, Attention(dim, heads = heads, dim_head = dim_head, dropout = dropout)),
PreNorm(dim, FeedForward(dim, mlp_dim, dropout=dropout))
]))
def forward(self, x):
for attn, ff in self.layers:
x = attn(x) + x
x = ff(x) + x
return x
- 此函数调用其他函数,构建整个Transformer Encoder模块
depth表示Transformer Encoder模块的迭代次数,即原文示例图中的参数L
ViT
class ViT(nn.Module):
def __init__(self, *, image_size, patch_size, num_classes, dim, depth, heads, mlp_dim, pool = 'cls', channels = 3, dim_head = 64, dropout = 0., emb_dropout = 0.):
super().__init__()
image_height, image_width = pair(image_size)
patch_height, patch_width = pair(patch_size)
assert image_height % patch_height == 0 and image_width % patch_width == 0
num_patches = (image_height // patch_height) * (image_width // patch_width)
patch_dim = channels * patch_height * patch_width
assert pool in {'cls', 'mean'}
self.to_patch_embedding = nn.Sequential(
Rearrange('b c (h p1)(w p2) -> b (h w)(p1 p2 c)', p1 = patch_height, p2 = patch_width),
nn.Linear(patch_dim, dim)
)
self.pos_embedding = nn.Parameter(torch.randn(1, num_patches + 1, dim))
self.cls_token = nn.Parameter(torch.randn(1, 1, dim))
self.dropout = nn.Dropout(emb_dropout)
self.transformer = Transformer(dim, depth, heads, dim_head, mlp_dim, dropout)
self.pool = pool
self.to_latent = nn.Identity()
self.mlp_head = nn.Sequential(
nn.LayerNorm(dim),
nn.Linear(dim, num_classes)
)
def forward(self, img):
x = self.to_patch_embedding(img)
b, n, _ = x.shape
cls_tokens = repeat(self.cls_token, '() n d -> b n d', b = b)
x = torch.cat((cls_tokens, x), dim = 1)
x += self.pos_embedding[:, :(n+1)]
x = self.dropout(x)
x = self.transformer(x)
x = x.mean(dim = 1) if self.pool == 'mean' else x[:, 0]
x = self.to_latent(x)
print(x.shape)
return self.mlp_head(x)
-
该函数组合各函数并最终实现ViT算法
- $$ z_0 = [x_{class}; x_p^1E; x_p^2E; ...; x_p^NE] + E_{pos}, \quad E \in \mathbb{R}^{(P^2 \cdot C) \times D}, E_{pos} \in \mathbb{R}^{(P^2 \cdot C) \times D} $$
-
positioal embedding 和 class token 由
nn.Parameter()定义。如对该函数感到疑问,请移步参考博客